Quin número hauria de seguir a la següent sèrie i per què?
Com sempre, a tota persona que doni una solució diferent de la que tinc en ment però amb sentit, li donaré el puntet, faltaria més!
(Espero no equivocar-me posant la sèrie...)
24, 38, 39, 52, 53, 54, 57, 59, 61, 62, 64, 68
Setmana anterior
Setmana següent
diumenge, 25 de desembre del 2005
diumenge, 18 de desembre del 2005
El problema de la setmana - 8 dames
Aquesta setmana el problema me'l proposa l'escaquejant. El problema està tret del Museo Elder de ciencia y tecnología de les Palmes de Gran Canària (realment, la pàgina web del museu també és molt interessant).
El problema consisteix en col.locar 3 dames blanques i 5 dames negres en un tauler 5x5 de forma que cap dama blanca amenaci cap dama negra (i, és clar, si cap dama blanca amenaça cap dama negra, tampoc cap dama negra amenaçarà cap dama blanca).
El problema estarà vigent una mica més d'una setmana. El proper problema, el dia 27 (o si puc abans, el dia 25, però dubto que pugui).
Aprofito el post del problema de la setmana per informar que he posat un sudoku diari aquí a la columna de la dreta, per si algú s'avorreix durant les festes de Nadal o durant l'any. La columna és tan gran que al final ja ocuparà més que els posts, però es va omplint dia rere dia.
Setmana anterior
Setmana següent
El problema consisteix en col.locar 3 dames blanques i 5 dames negres en un tauler 5x5 de forma que cap dama blanca amenaci cap dama negra (i, és clar, si cap dama blanca amenaça cap dama negra, tampoc cap dama negra amenaçarà cap dama blanca).
El problema estarà vigent una mica més d'una setmana. El proper problema, el dia 27 (o si puc abans, el dia 25, però dubto que pugui).
Aprofito el post del problema de la setmana per informar que he posat un sudoku diari aquí a la columna de la dreta, per si algú s'avorreix durant les festes de Nadal o durant l'any. La columna és tan gran que al final ja ocuparà més que els posts, però es va omplint dia rere dia.
Setmana anterior
Setmana següent
divendres, 16 de desembre del 2005
Calendari
Aquest és el meu calendari de sobretaula de l'any 2005. Ja està a punt de jubilar-se, però segur que aviat tindrà un substitut:
Com es pot observar, el calendari és un dodecaedre regular. La gràcia de fer-ho amb un dodecaedre és que, com ja diu el nom, el poliedre ja té 12 cares, i així s'aprofita una cara per cada mes :-)
La foto no és massa bona, però es pot observar que el calendari està escrit en català i no és difícil de construir. Simplement, es pot anar aquí i imprimir-se el model. Una mica de treball manual i el calendari ja estarà fet. Fàcil i barat.
A mi m'agrada més el model amb el dodecaedre regular (on les cares són pentàgons regulars), però també hi ha un model amb les cares romboidals.
Com es pot observar, el calendari és un dodecaedre regular. La gràcia de fer-ho amb un dodecaedre és que, com ja diu el nom, el poliedre ja té 12 cares, i així s'aprofita una cara per cada mes :-)
La foto no és massa bona, però es pot observar que el calendari està escrit en català i no és difícil de construir. Simplement, es pot anar aquí i imprimir-se el model. Una mica de treball manual i el calendari ja estarà fet. Fàcil i barat.
A mi m'agrada més el model amb el dodecaedre regular (on les cares són pentàgons regulars), però també hi ha un model amb les cares romboidals.
dimecres, 14 de desembre del 2005
Calculadora del google
Ja fa temps que el google es pot usar com a calculadora. És una cosa que em pensava que sabia molta gent, però cada cop que ho comento amb algú, així de passada, veig que la gent no ho sap. Així que, per començar, diré que el google es pot usar com a calculadora. Simplement, en comptes de posar el que es vulgui buscar, es posa una operació matemàtica i ell te la fa.
Que vols saber quant són 2+3? Doncs li preguntes al google i ell t'ho diu. Que vols fer coses més complicades com calcular quants grams de sorra havia de pagar el rei a l'inventor dels escacs? Doncs se li pregunta al google, i ell et contesta. Una arrel quadrada? Cap problema. El logaritme neperià de pi? Només l'has de demanar. Molt més potent que la calculadora del windows.
Però hi ha un problema. Què passa si li poses una cosa bastant senzilla, com 1-0.8-0.2? Val la pena mirar-ho. I després, comprovar què passa si es calcula 1-0.2-0.8. Hauria de sortir el mateix, veritat? Però...
Com que això corre com l'escuma i tots quan rebem el mail que ho explica anem al google a mirar-ho, potser els del google s'adonen que hi ha massa gent provant la mateixa operació. Així que poso el que m'ha sortit quan he fet 1-0.8-0.2. Perquè en quedi constància:

Vaja, de l'estil de 1+1=3, per valors grans d'1 :-)
Que vols saber quant són 2+3? Doncs li preguntes al google i ell t'ho diu. Que vols fer coses més complicades com calcular quants grams de sorra havia de pagar el rei a l'inventor dels escacs? Doncs se li pregunta al google, i ell et contesta. Una arrel quadrada? Cap problema. El logaritme neperià de pi? Només l'has de demanar. Molt més potent que la calculadora del windows.
Però hi ha un problema. Què passa si li poses una cosa bastant senzilla, com 1-0.8-0.2? Val la pena mirar-ho. I després, comprovar què passa si es calcula 1-0.2-0.8. Hauria de sortir el mateix, veritat? Però...
Com que això corre com l'escuma i tots quan rebem el mail que ho explica anem al google a mirar-ho, potser els del google s'adonen que hi ha massa gent provant la mateixa operació. Així que poso el que m'ha sortit quan he fet 1-0.8-0.2. Perquè en quedi constància:

Vaja, de l'estil de 1+1=3, per valors grans d'1 :-)
dissabte, 3 de desembre del 2005
El problema de la setmana - partida més curta
Aquest cop el problema de la setmana serà el problema quinzenal, perquè properament marxo a jugar el campionat de Catalunya femení. Així doncs, aquest problema estarà vigent fins el dia 18 de desembre.
De mentres, i si algú s'avorreix, suposo que podrà mirar les partides a través del portal de retransmissions de la federació catalana d'escacs, des de dimarts 6 fins a diumenge 11. Accepto qualsevol comentari del tipus "però mira que ets dolenta!" sempre i quan sigui crítica constructiva.
Continuo amb el problema de la setmana. Per començar, anuncio que ramtia ha aconseguit resoldre el test lògic just el dia abans que aquest complís un any. A més, en FreshMind ha proposat un problema, que està als comentaris del problema de la setmana anterior. Com a resum, el problema seria el següent: ¿Cuál es la única palabra q se escribe como es? Hi ha l'explicació del que vol dir als comentaris del post anterior, com ja he dit. Jo no tinc idea de què és, de moment, però si algú ho sap i en FreshMind ho confirma, li donaré també un punt.
I ara el problema (ja era hora). Es tracta de la variació d'un joc que vaig veure fa un temps ara no recordo on. Es juga en un tauler d'escacs, i amb les peces d'escacs. Es comença amb el tauler buit i a cada torn, cada jugador posa una peça al tauler. Cada jugador només té les peces d'un joc d'escacs (o sigui, només disposa d'un rei, una dama, dues torres, dos àlfils, dos cavalls i vuit peons). Per posar una peça al tauler, s'ha de complir que la peça no es posi a cap casella amenaçada per cap peça contrària i que no amenaci a cap peça contrària. Perd el jugador que ha de jugar i no pot col.locar cap peça.
Per exemple, si les blanques posen una dama a d4, aleshores les negres poden posar un rei a e6, però no a e5. A e6 hi poden posar qualsevol peça excepte un cavall, perquè aleshores amenaçaria la dama blanca. Si per exemple posen un rei a e6, les blanques poden posar per exemple un àlfil a e3, però no hi poden posar una torre.
El problema consisteix a trobar la partida més curta que es pugui jugar amb aquest joc. Jo no sé la solució. Així que el dia 18 de desembre donaré un punt a la persona que hagi aconseguit la partida més curta (a igualtat de llargada, li donaré al primer que hagi trobat la partida). A veure si aquesta setmana també trobeu el problema tan fàcil :-)
Per qualsevol dubte, seré per aquí fins dilluns al vespre (o potser dimarts al matí) i a partir del dia 11 o 12.
Setmana anterior
Setmana següent
De mentres, i si algú s'avorreix, suposo que podrà mirar les partides a través del portal de retransmissions de la federació catalana d'escacs, des de dimarts 6 fins a diumenge 11. Accepto qualsevol comentari del tipus "però mira que ets dolenta!" sempre i quan sigui crítica constructiva.
Continuo amb el problema de la setmana. Per començar, anuncio que ramtia ha aconseguit resoldre el test lògic just el dia abans que aquest complís un any. A més, en FreshMind ha proposat un problema, que està als comentaris del problema de la setmana anterior. Com a resum, el problema seria el següent: ¿Cuál es la única palabra q se escribe como es? Hi ha l'explicació del que vol dir als comentaris del post anterior, com ja he dit. Jo no tinc idea de què és, de moment, però si algú ho sap i en FreshMind ho confirma, li donaré també un punt.
I ara el problema (ja era hora). Es tracta de la variació d'un joc que vaig veure fa un temps ara no recordo on. Es juga en un tauler d'escacs, i amb les peces d'escacs. Es comença amb el tauler buit i a cada torn, cada jugador posa una peça al tauler. Cada jugador només té les peces d'un joc d'escacs (o sigui, només disposa d'un rei, una dama, dues torres, dos àlfils, dos cavalls i vuit peons). Per posar una peça al tauler, s'ha de complir que la peça no es posi a cap casella amenaçada per cap peça contrària i que no amenaci a cap peça contrària. Perd el jugador que ha de jugar i no pot col.locar cap peça.
Per exemple, si les blanques posen una dama a d4, aleshores les negres poden posar un rei a e6, però no a e5. A e6 hi poden posar qualsevol peça excepte un cavall, perquè aleshores amenaçaria la dama blanca. Si per exemple posen un rei a e6, les blanques poden posar per exemple un àlfil a e3, però no hi poden posar una torre.
El problema consisteix a trobar la partida més curta que es pugui jugar amb aquest joc. Jo no sé la solució. Així que el dia 18 de desembre donaré un punt a la persona que hagi aconseguit la partida més curta (a igualtat de llargada, li donaré al primer que hagi trobat la partida). A veure si aquesta setmana també trobeu el problema tan fàcil :-)
Per qualsevol dubte, seré per aquí fins dilluns al vespre (o potser dimarts al matí) i a partir del dia 11 o 12.
Setmana anterior
Setmana següent
diumenge, 27 de novembre del 2005
El problema de la setmana - agència de viatges
Aquesta setmana el problema pot semblar una mica estrany. Pot semblar que no té solució. Però sí que en té, i és una solució lògica. Cal donar la solució i explicar el perquè. No sé si hi ha alguna altra solució, però tota solució raonada, i amb sentit (a part de la que espero) tindrà un punt. A veure si el problema triga una mica més...
Aquesta última setmana una agència de viatges ha fet 32 reserves per Tenerife, 30 per Menorca i 18 per Ibiza. Quantes reserves ha fet per Portugal?
Setmana anterior
Setmana següent
Aquesta última setmana una agència de viatges ha fet 32 reserves per Tenerife, 30 per Menorca i 18 per Ibiza. Quantes reserves ha fet per Portugal?
Setmana anterior
Setmana següent
diumenge, 20 de novembre del 2005
El problema de la setmana - culpables
Ens trobem en un cas d'assassinat (o del que es vulgui), on hi ha 4 acusats. Sabem que:
- Si A és culpable, aleshores B és còmplice.
- Si B és culpable, aleshores o bé C és còmplice o bé A és innocent.
- Si D és innocent, aleshores A és culpable i C innocent.
- Si D és culpable, també ho és A.
Qui és innocent i qui és culpable? (Tenint en compte que els còmplices són culpables, és clar!)
Setmana anterior
Setmana següent
- Si A és culpable, aleshores B és còmplice.
- Si B és culpable, aleshores o bé C és còmplice o bé A és innocent.
- Si D és innocent, aleshores A és culpable i C innocent.
- Si D és culpable, també ho és A.
Qui és innocent i qui és culpable? (Tenint en compte que els còmplices són culpables, és clar!)
Setmana anterior
Setmana següent
diumenge, 13 de novembre del 2005
El problema de la setmana - número de telèfon
Aquesta setmana es tracta de buscar un número de telèfon que consta d'un prefixe de 3 xifres i 4 xifres més.
Les condicions són les següents:
- El número format per les xifres que estan a les posicions 4 i 5 és un quadrat perfecte.
- El número format per les xifres de les posicions 5 i 6 també és un quadrat perfecte.
- El número format per les xifres de les posicions 6 i 7 també és un quadrat perfecte.
- El prefixe és un cub perfecte.
- El producte dels dígits del número pròpiament dit (o sigui, les xifres que estan a les posicions 4, 5, 6 i 7) dóna el prefixe.
Quin és el número?
Setmana anterior
Setmana següent
Les condicions són les següents:
- El número format per les xifres que estan a les posicions 4 i 5 és un quadrat perfecte.
- El número format per les xifres de les posicions 5 i 6 també és un quadrat perfecte.
- El número format per les xifres de les posicions 6 i 7 també és un quadrat perfecte.
- El prefixe és un cub perfecte.
- El producte dels dígits del número pròpiament dit (o sigui, les xifres que estan a les posicions 4, 5, 6 i 7) dóna el prefixe.
Quin és el número?
Setmana anterior
Setmana següent
dissabte, 12 de novembre del 2005
Coronar cavall
A la següent posició:
semblaria que se'n va dels dits jugar 1. c8 = D+, però no serveix per guanyar. La única forma de guanyar és coronant un tercer cavall! (Amb un escac previ, és clar). La forma de guanyar és la següent:
1. Cb3+ Rb6
Si 1. ... Rc4 2. Cd2+ guanyant
Si 1. ... Rb5/Rd5 2. Cc3+ guanyant
2. c8=C+!
2. c8=D+ no guanya per 2. ... Df5+ 3. Rd8 Df8+ 4. Rd7 Df5+ i taules per repetició.
2. ... Rb5
Si 2. ... Ra6 3. Cc5+
Si 2. ... Rb7 3. Cd6+
3. Cd6+ Ra4
4. Cc5+
I el final de 3 cavalls contra 2 es guanya. Difícil? Una mica... Li acabo de guanyar ara fa un moment al Fritz, però m'ha costat una mica de suor. Suposo que amb pràctica es deu acabar guanyant fàcil. Només s'ha d'acabar arraconant el rei i donar-li mat. Per exemple, amb els cavalls a b4 i c4 i el rei a e2, l'altre rei (si s'ha aconseguit arraconar-lo) només es pot moure per les caselles a1-c1, mentre amb l'altre cavall t'acostes a fer mat. Tampoc em posaré a estudiar ara el mat amb 3 cavalls (ara ve quan d'aquí a poc em trobo amb la situació i gairebé sense temps per pensar com fer el mat). Però si a algú li interessa, i perquè m'ha agradat com queda estèticament, el mat que he aconseguit fer és el següent:
Seguint amb el tema del post, que és coronar cavall, un altre exemple és la següent posició:
Altre cop, la única forma de guanyar el coronar cavall i acabar amb un final de 3 cavalls contra 1 (al final m'ho pensaré seriosament, això del mat amb 3 cavalls...)
1.f5 Rg5
2. f6 Rg6
3. Rg8 Ce3
4. f7 Cg4
5. f8=C+!
La única forma de guanyar (si és que se'n sap). Si 5. f8 = D Ch6+ 6. Rh8 Cf7+, amb escac continu.
Que són excepcions? Sí, és clar, però què seria el món sense excepcions? A més, aquí n'hi ha una altra:
Està clar que aquí f8=D no serveix per Ce6+. Qualsevol jugada que no sigui f8 = C, segueix amb Ce6+ o Cf7. Així que la única possibilitat de guanyar és jugar 1. f8=C. Un cop fet això, posaré un exemple de com podria ser el mat:
1. ... Ce4 2. Ce6+ Rb7 3. Rf7 Ra6 4. Cd4 Rb7 5. Re7 Cc5 6. Cf7 Rc7 7. Cfd6 Ca4 8. C6b5+ Rb7 9. Rd8 Cc5 10. Cbd6+ Ra7 11. Rc8 Cd3 12. Cc6+ Ra6 13. Cb8+ Ra7 14. Cb5+ Ra8 15. Cb6 mat.
Ja per acabar, un problema amb ajuda. L'ajuda és que per guanyar es necessita coronar cavall :-) i així el problema és molt fàcil, però per no escriure-ho tot jo:
Juguen blanques i malgrat l'amenaça de mat, guanyen:
Per què no val 1. Th8+ Rh8 2. f8=D+?

semblaria que se'n va dels dits jugar 1. c8 = D+, però no serveix per guanyar. La única forma de guanyar és coronant un tercer cavall! (Amb un escac previ, és clar). La forma de guanyar és la següent:
1. Cb3+ Rb6
Si 1. ... Rc4 2. Cd2+ guanyant
Si 1. ... Rb5/Rd5 2. Cc3+ guanyant
2. c8=C+!
2. c8=D+ no guanya per 2. ... Df5+ 3. Rd8 Df8+ 4. Rd7 Df5+ i taules per repetició.
2. ... Rb5
Si 2. ... Ra6 3. Cc5+
Si 2. ... Rb7 3. Cd6+
3. Cd6+ Ra4
4. Cc5+
I el final de 3 cavalls contra 2 es guanya. Difícil? Una mica... Li acabo de guanyar ara fa un moment al Fritz, però m'ha costat una mica de suor. Suposo que amb pràctica es deu acabar guanyant fàcil. Només s'ha d'acabar arraconant el rei i donar-li mat. Per exemple, amb els cavalls a b4 i c4 i el rei a e2, l'altre rei (si s'ha aconseguit arraconar-lo) només es pot moure per les caselles a1-c1, mentre amb l'altre cavall t'acostes a fer mat. Tampoc em posaré a estudiar ara el mat amb 3 cavalls (ara ve quan d'aquí a poc em trobo amb la situació i gairebé sense temps per pensar com fer el mat). Però si a algú li interessa, i perquè m'ha agradat com queda estèticament, el mat que he aconseguit fer és el següent:

Seguint amb el tema del post, que és coronar cavall, un altre exemple és la següent posició:

Altre cop, la única forma de guanyar el coronar cavall i acabar amb un final de 3 cavalls contra 1 (al final m'ho pensaré seriosament, això del mat amb 3 cavalls...)
1.f5 Rg5
2. f6 Rg6
3. Rg8 Ce3
4. f7 Cg4
5. f8=C+!
La única forma de guanyar (si és que se'n sap). Si 5. f8 = D Ch6+ 6. Rh8 Cf7+, amb escac continu.
Que són excepcions? Sí, és clar, però què seria el món sense excepcions? A més, aquí n'hi ha una altra:

Està clar que aquí f8=D no serveix per Ce6+. Qualsevol jugada que no sigui f8 = C, segueix amb Ce6+ o Cf7. Així que la única possibilitat de guanyar és jugar 1. f8=C. Un cop fet això, posaré un exemple de com podria ser el mat:
1. ... Ce4 2. Ce6+ Rb7 3. Rf7 Ra6 4. Cd4 Rb7 5. Re7 Cc5 6. Cf7 Rc7 7. Cfd6 Ca4 8. C6b5+ Rb7 9. Rd8 Cc5 10. Cbd6+ Ra7 11. Rc8 Cd3 12. Cc6+ Ra6 13. Cb8+ Ra7 14. Cb5+ Ra8 15. Cb6 mat.
Ja per acabar, un problema amb ajuda. L'ajuda és que per guanyar es necessita coronar cavall :-) i així el problema és molt fàcil, però per no escriure-ho tot jo:
Juguen blanques i malgrat l'amenaça de mat, guanyen:

Per què no val 1. Th8+ Rh8 2. f8=D+?
diumenge, 6 de novembre del 2005
El problema de la setmana - Espelmes
Tenim dues metxes. Cadascuna triga una hora a consumir-se del tot. No tenim cap rellotge i volem comptar un quart d'hora exacte, utilitzant només les metxes. No podem trencar les metxes de cap manera, només encendre-les.
Com ens ho podem fer per comptar un quart d'hora?
Setmana anterior
Setmana següent
Com ens ho podem fer per comptar un quart d'hora?
Setmana anterior
Setmana següent
dilluns, 31 d’octubre del 2005
Mat en quatre
A la següent posició, el blanc pot fer mat en quatre jugades de més d'una manera. De quantes maneres pot fer mat?
A part, poso la solució a l'últim problema que vaig posar, que es va quedar com una mica abandonat.

A part, poso la solució a l'últim problema que vaig posar, que es va quedar com una mica abandonat.
dissabte, 29 d’octubre del 2005
El problema de la setmana - 64
Aquesta setmana el problema consisteix a escriure el número 64 utilitzant només dues vegades el número 4. A part dels dos quatres, es poden utilitzar tots els símbols matemàtics que es vulguin (suma, resta, multiplicació, divisió, potències, logaritmes, arrels, factorials...) sempre i quan els únics números que hi apareguin sigui dos quatres.
Setmana anterior
Setmana següent
Setmana anterior
Setmana següent
dilluns, 24 d’octubre del 2005
Creuar el riu
Aquí hi podreu trobar un d'aquells jocs de creuar el riu. No és excessivament difícil (en 4 o 5 minuts surt la solució fàcil) però és entretingut.
Es tracta d'una família amb els pares, dos nens i dues nenes. A més, hi ha un lladre i un policia. Les regles per passar la gent a l'altra banda del riu són les següents:
- El pare no es pot quedar amb cap nena si no hi ha la mare (ni a cap banda de riu ni a la barca).
- La mare no es pot quedar amb cap nen si no hi ha el pare (ni a cap banda de riu ni a la barca).
- El lladre no es pot quedar amb cap membre de la família si no hi ha el policia (ni a cap banda de riu ni a la barca).
- La barca només té lloc per dues persones.
- Només poden conduir la barca el pare, la mare i el policia.
Per entrar, s'ha de clicar el link de dalt i prémer el botó blau.
Es tracta d'una família amb els pares, dos nens i dues nenes. A més, hi ha un lladre i un policia. Les regles per passar la gent a l'altra banda del riu són les següents:
- El pare no es pot quedar amb cap nena si no hi ha la mare (ni a cap banda de riu ni a la barca).
- La mare no es pot quedar amb cap nen si no hi ha el pare (ni a cap banda de riu ni a la barca).
- El lladre no es pot quedar amb cap membre de la família si no hi ha el policia (ni a cap banda de riu ni a la barca).
- La barca només té lloc per dues persones.
- Només poden conduir la barca el pare, la mare i el policia.
Per entrar, s'ha de clicar el link de dalt i prémer el botó blau.
diumenge, 23 d’octubre del 2005
El problema de la setmana - 3 números
Es tracta de trobar tres números (enters i positius, per si de cas) que compleixin la propietat que si es multipliquen dos dels números i es divideixen pel tercer, sempre dóna 1 com a residu.
Per exemple, si tenim 1, 2 i 3, si multipliquem 3*1=3 i dividim per 2, dóna 1 com a residu. Però aquests números no ho compleixen, perquè si multipliquem 2*1=2, i al dividir per 3 dóna 2 com a residu.
Setmana anterior
Setmana següent
Per exemple, si tenim 1, 2 i 3, si multipliquem 3*1=3 i dividim per 2, dóna 1 com a residu. Però aquests números no ho compleixen, perquè si multipliquem 2*1=2, i al dividir per 3 dóna 2 com a residu.
Setmana anterior
Setmana següent
diumenge, 16 d’octubre del 2005
Cadena més llarga
El problema de la setmana passada va portar una mica de polèmica, perquè jo vaig llegir per sobre com era la solució, i al final va resultar que ho havia llegit una mica malament.
Abans de començar amb la cadena de tres símbols, es comença amb una cadena de dos símbols, anomenada sèrie de Thue. Es comença per 01 i a cada pas es substitueix cada 0 per 01 i cada 1 per 10. Així, s'obtenen cadenes, cada cop del doble de longitud de l'anterior:
01
0110
01101001
0110100110010110
Com es pot observar, cada cadena té el doble de longitud que la anterior i, a més, la primera meitat de cada cadena és exactament la cadena anterior.
Aquestes cadenes compleixen (faig un acte de fe i m'ho crec) que cap bloc d'un o més dígits es repeteix 3 vegades consecutives. Es poden repetir dos cops, però mai tres.
Com que aquest pas de canviar els 0 per 01 i els 1 per 10 es pot fer tantes vegades com es vulgui, aquesta sèrie es pot aconseguir amb el nombre de dígits que es vulgui.
Aleshores, per aconseguir la sèrie desitjada, només cal substituir els 00 i 11 per 1, els 10 per 2 i els 01 per 3. Així, la sèrie que surt compleix la propietat (segons el llibre, jo faig un acte de fe). I com que la sèrie de Thue és infinita, aquesta també ho serà.
En el cas de l'exemple, la sèrie seria:
312321312132312
I així se'n pot construir una tan llarga com es vulgui.
Abans de començar amb la cadena de tres símbols, es comença amb una cadena de dos símbols, anomenada sèrie de Thue. Es comença per 01 i a cada pas es substitueix cada 0 per 01 i cada 1 per 10. Així, s'obtenen cadenes, cada cop del doble de longitud de l'anterior:
01
0110
01101001
0110100110010110
Com es pot observar, cada cadena té el doble de longitud que la anterior i, a més, la primera meitat de cada cadena és exactament la cadena anterior.
Aquestes cadenes compleixen (faig un acte de fe i m'ho crec) que cap bloc d'un o més dígits es repeteix 3 vegades consecutives. Es poden repetir dos cops, però mai tres.
Com que aquest pas de canviar els 0 per 01 i els 1 per 10 es pot fer tantes vegades com es vulgui, aquesta sèrie es pot aconseguir amb el nombre de dígits que es vulgui.
Aleshores, per aconseguir la sèrie desitjada, només cal substituir els 00 i 11 per 1, els 10 per 2 i els 01 per 3. Així, la sèrie que surt compleix la propietat (segons el llibre, jo faig un acte de fe). I com que la sèrie de Thue és infinita, aquesta també ho serà.
En el cas de l'exemple, la sèrie seria:
312321312132312
I així se'n pot construir una tan llarga com es vulgui.
El problema de la setmana - suma de quadrats
Aquesta setmana el problema és molt fàcil (va com va...) Com que és tan fàcil i estic generosa, les respostes me les podeu enviar al mail de la dreta i donaré punts a tots els que l'encerteu.
Es tracta de trobar 9 números consecutius, de forma que si es sumen els quadrats dels cinc primers, dóna el mateix que si es sumen els quadrats dels quatre últims.
Si el problema fos per 5 números, la solució seria:
10^2+11^2+12^2=13^2+14^2
i si fos per 7 números:
21^2+22^2+23^2+24^2=25^2+26^2+27^2.
Setmana anterior
Setmana següent
Es tracta de trobar 9 números consecutius, de forma que si es sumen els quadrats dels cinc primers, dóna el mateix que si es sumen els quadrats dels quatre últims.
Si el problema fos per 5 números, la solució seria:
10^2+11^2+12^2=13^2+14^2
i si fos per 7 números:
21^2+22^2+23^2+24^2=25^2+26^2+27^2.
Setmana anterior
Setmana següent
diumenge, 9 d’octubre del 2005
El problema de la setmana - Cadena més llarga
Es tracta de trobar la cadena més llarga que es pot aconseguir amb el 1, 2 i 3 sense que es repeteixi cap seqüència de símbols seguits.
Si només es fes amb l'1 i el 2, la seqüència més llarga tindria 3 símbols: 121 (o 212). Després de l'1 no es pot posar un altre 1 perquè es repetiria la seqüència d'uns. Per tant, després de l'1 hi va un 2. Després del 2 no es pot posar un altre 2, perquè es repetiria la seqüència 2. Així que s'ha de posar un 1: 121. I després d'aquest 1 no es pot posar un 1 perquè es repetiria la seqüència d'1 seguida, ni tampoc es pot posar un 2 perquè es repetiria la seqüència 12.
Un cop vist l'exemple de l'1 i el 2, es tracta de fer el mateix amb el 1, el 2 i el 3. Donaré el punt a qui posi la seqüència més llarga, i en cas de que no sigui la seqüència més llarga, donaré un exemple de la seqüència més llarga.
Exemples correctes: 12312
121312
Exemples incorrectes: 123123
1231212
12321321
(Espero que s'hagi entès bé).
Setmana anterior
Setmana següent
Si només es fes amb l'1 i el 2, la seqüència més llarga tindria 3 símbols: 121 (o 212). Després de l'1 no es pot posar un altre 1 perquè es repetiria la seqüència d'uns. Per tant, després de l'1 hi va un 2. Després del 2 no es pot posar un altre 2, perquè es repetiria la seqüència 2. Així que s'ha de posar un 1: 121. I després d'aquest 1 no es pot posar un 1 perquè es repetiria la seqüència d'1 seguida, ni tampoc es pot posar un 2 perquè es repetiria la seqüència 12.
Un cop vist l'exemple de l'1 i el 2, es tracta de fer el mateix amb el 1, el 2 i el 3. Donaré el punt a qui posi la seqüència més llarga, i en cas de que no sigui la seqüència més llarga, donaré un exemple de la seqüència més llarga.
Exemples correctes: 12312
121312
Exemples incorrectes: 123123
1231212
12321321
(Espero que s'hagi entès bé).
Setmana anterior
Setmana següent
dijous, 6 d’octubre del 2005
Ofegat
A l'any 1958, Chalomeiev i Gurin van arribar a la següent posició:
És el torn de les negres (està clar que si juguessin les blanques, guanyen amb Dd1#)
En aquest moment, Gurin va jugar 1. ... g1 i va deixar el peó a la vuitena fila sense reemplaçar-lo per cap altra peça. Quan Chalomeiev li va preguntar quina peça volia, va dir que volia una dama, però no va reemplaçar el peó per la dama.
Abans que la dama es posés a la casella g1, Chalomeiev va jugar 2. Dd1+! i, després de 2. ... Dxd1, el rei blanc està ofegat.
En aquest moment, l'àrbitre va intervenir i va dir que, com que no havia reemplaçat el peó per la dama, la jugada no estava acabada i el negre havia d'acabar la jugada. Li va demanar a Gurin quina peça volia. Gurin, tot content, va reemplaçar el peó per una torre. Acte seguit, Chalomeiev va jugar 2. Db5+! El negre s'ha de menjar la dama, i el rei blanc torna a estar ofegat!

És el torn de les negres (està clar que si juguessin les blanques, guanyen amb Dd1#)
En aquest moment, Gurin va jugar 1. ... g1 i va deixar el peó a la vuitena fila sense reemplaçar-lo per cap altra peça. Quan Chalomeiev li va preguntar quina peça volia, va dir que volia una dama, però no va reemplaçar el peó per la dama.
Abans que la dama es posés a la casella g1, Chalomeiev va jugar 2. Dd1+! i, després de 2. ... Dxd1, el rei blanc està ofegat.
En aquest moment, l'àrbitre va intervenir i va dir que, com que no havia reemplaçat el peó per la dama, la jugada no estava acabada i el negre havia d'acabar la jugada. Li va demanar a Gurin quina peça volia. Gurin, tot content, va reemplaçar el peó per una torre. Acte seguit, Chalomeiev va jugar 2. Db5+! El negre s'ha de menjar la dama, i el rei blanc torna a estar ofegat!
dimarts, 4 d’octubre del 2005
On és l'error?
Aquí hi ha diferents "demostracions" de coses que, òbviament, tenen algun error. Es tracta de saber quin és l'error.
Com que hi intervenen símbols matemàtics i no tinc ni idea de com posar-los en html i no tenia ganes de fer un pdf i enllaçar al pdf, ho he escrit a mà i ho he escanejat. Ja per endavant demano perdó per si algú no entèn la meva lletra. De totes formes, clicant a sobre la imatge, es veurà més gran.
Error 1: 1=2
El primer cop que vaig veure aquesta demostració d'1=2 feia primer de BUP. Així que és bastant fàcil veure on és el problema:
Errors 2: 0=1
Aquesta me l'han ensenyat avui. Just després de veure-la, m'ha recordat el segon error de 0=1, que acostumo a explicar a classe. Així que tant aquesta com la següent tenen el mateix error. I les dues "demostren" que 0=1.
Per no posar aquí la següent demostració de 0=1 seguida, poso una anècdota bastant coneguda d'en Bertand Russell, però per si algú no la coneix. Un dia estava al bar amb uns amics i va dir que si li deixaven admetre que 1+1=1, aleshores, podria demostrar qualsevol cosa. Aleshores un amic seu li va dir: "D'acord, suposa que 1+1=1 i demostra que ets el Papa". En Bertand Russell va contestar, sense pensar un moment: "Jo sóc una persona, el Papa també és una persona. Junts som 1+1 persones. Com que 1+1=1, els dos som una sola persona, i per tant, jo sóc el Papa".
Error 3: 1=-1
Ja per acabar, aquesta "demostració" que em va portar una alumna de classes particulars ahir al matí:
Com que hi intervenen símbols matemàtics i no tinc ni idea de com posar-los en html i no tenia ganes de fer un pdf i enllaçar al pdf, ho he escrit a mà i ho he escanejat. Ja per endavant demano perdó per si algú no entèn la meva lletra. De totes formes, clicant a sobre la imatge, es veurà més gran.
Error 1: 1=2
El primer cop que vaig veure aquesta demostració d'1=2 feia primer de BUP. Així que és bastant fàcil veure on és el problema:
Errors 2: 0=1
Aquesta me l'han ensenyat avui. Just després de veure-la, m'ha recordat el segon error de 0=1, que acostumo a explicar a classe. Així que tant aquesta com la següent tenen el mateix error. I les dues "demostren" que 0=1.
Per no posar aquí la següent demostració de 0=1 seguida, poso una anècdota bastant coneguda d'en Bertand Russell, però per si algú no la coneix. Un dia estava al bar amb uns amics i va dir que si li deixaven admetre que 1+1=1, aleshores, podria demostrar qualsevol cosa. Aleshores un amic seu li va dir: "D'acord, suposa que 1+1=1 i demostra que ets el Papa". En Bertand Russell va contestar, sense pensar un moment: "Jo sóc una persona, el Papa també és una persona. Junts som 1+1 persones. Com que 1+1=1, els dos som una sola persona, i per tant, jo sóc el Papa".
Error 3: 1=-1
Ja per acabar, aquesta "demostració" que em va portar una alumna de classes particulars ahir al matí:
diumenge, 2 d’octubre del 2005
El problema de la setmana - Quadrat antimàgic
Tinc pendent un post sobre els quadrats màgics, que acabaré d'escriure un any d'aquests. De totes formes, més o menys tothom sap què són els quadrats màgics: són quadrats amb nxn cel.les, on hi ha disposats els nombres des de l'1 fins a l'n^2, i on totes les files, columnes i diagonals sumen el mateix. Per exemple, el següent és un quadrat màgic 3x3:
8 1 6
3 5 7
4 9 2
Però el problema d'aquesta setmana no va de quadrats màgics, sinó de quadrats antimàgics. Un quadrat antimàgic també conté els nombres des de l'1 fins a l'n^2. La única diferència és que si sumem les files, columnes i diagonals principals, totes sumen diferent (o sigui, no hi ha cap fila que sumi el mateix que cap altra fila, columna o diagonal, i el mateix per columnes i diagonals).
No posaré cap exemple, el problema de la setmana consisteix a trobar una solució de quadrat antimàgic 3x3. El problema també té una restricció, que a més de fer que la solució sigui única (llevat de rotacions i simetries) també és una solució maca.
Es tracta de trobar un quadrat antimàgic de forma que per passar d'un nombre al següent, només es pugui fer passant a una cel.la adjacent en horitzontal o vertical (no en diagonal). Això redueix molt el número de possibilitats. Un exemple, que no seria un quadrat antimàgic, d'això seria:
9 8 7
2 3 6
1 4 5
Setmana anterior
Setmana següent
8 1 6
3 5 7
4 9 2
Però el problema d'aquesta setmana no va de quadrats màgics, sinó de quadrats antimàgics. Un quadrat antimàgic també conté els nombres des de l'1 fins a l'n^2. La única diferència és que si sumem les files, columnes i diagonals principals, totes sumen diferent (o sigui, no hi ha cap fila que sumi el mateix que cap altra fila, columna o diagonal, i el mateix per columnes i diagonals).
No posaré cap exemple, el problema de la setmana consisteix a trobar una solució de quadrat antimàgic 3x3. El problema també té una restricció, que a més de fer que la solució sigui única (llevat de rotacions i simetries) també és una solució maca.
Es tracta de trobar un quadrat antimàgic de forma que per passar d'un nombre al següent, només es pugui fer passant a una cel.la adjacent en horitzontal o vertical (no en diagonal). Això redueix molt el número de possibilitats. Un exemple, que no seria un quadrat antimàgic, d'això seria:
9 8 7
2 3 6
1 4 5
Setmana anterior
Setmana següent
dijous, 29 de setembre del 2005
Mat en dues
En la següent posició juguen les blanques i fan mat en dues.
De quantes formes diferents es pot fer el mat en dues?
De quantes formes diferents es pot fer el mat en dues?

dissabte, 24 de setembre del 2005
Finals de peons
Començo mirant el següent final de peons:
En aquest cas juguen blanques. Les blanques tenen un peó a sisena, mentre que el de les negres està a segona. En principi, això seria bo pel blanc, però si ens mirem una mica millor la posició, veiem que el peó de b6 es perd irremediablement. Si el blanc intenta anar a defensar-lo, 1. Rf4 Rd3 2. Re5 Rc4 3. Rd6 Rb5 4. Rc7, el negre el guanya simplement jugant Ra6.
Així doncs, amb el peó de b6 perdut, el blanc intentarà fer taules. Però, com s'aconsegueixen les taules? Doncs la forma de fer-ho és col.locant-se a b4 just quan el rei negre acabi de menjar el peó de b6. Per tant, l'objectiu del blanc és poder arribar a b4. I quina és la forma més ràpida d'arribar-hi? Doncs, encara que sembli mentida, la forma més ràpida d'arribar-hi és mitjançant les diagonals g3-e1 i e1-b4.
Ja hem vist que amb Rf4 no s'aconseguia arribar a b4 a temps. I què passaria si el blanc jugués 1. Rf3, que en principi està més a prop de b4 que f2? Si el blanc jugués 1. Rf3, el negre podria jugar 1. ... Rd3! tapant el pas del blanc cap a b4.
Així que la única solució és 1. Rf2! Rd3 2. Re1 Rc4 3. Rd2 Rb5 4. Rc3 Rxb6 i arribem a temps a jugar 5. Rb4 taules. Si el negre ens hagués volgut tapar la diagonal jugant 1. ... Rd2, simplement juguem 2. Rf1. A 2. ... Rd3 o Rc3 es contesta 3. Re1, com abans, arribant a temps a b4. A 2. ... Rd1 es contesta 3. Rf2 i també s'arriba a temps a b4.
El següent final és semblant al que acabo d'explicar:
El peó negre d'h7 està perdut. Així doncs, les negres no poden aspirar a res més que a fer taules. Per fer taules, han d'aconseguir portar el seu rei a f7 just en el moment en què les blanques mengin el peó d'a7. Per fer-ho, altra vegada s'ha d'utilitzar una diagonal, en aquest cas la diagonal a2-g8.
Si el negre jugués 1. ... Rc1, perderia i no podria arribar a f7 a temps: 2. Rc3! Rb1 3. Rd4 Rc2 4. Re5 Rd3 5. Rf6 Re4 6. Rg7 Rf5 7. Rxh7 Rf6 8. Rg8.
Però el negre pot aconseguir les taules mitjançant 1. ... Ra1! 2. Rc3 Ra1 3. Rd4 Rb3 4. Re5 Rc4 5. Rf6 Rd5 6. Rg7 Re6 7. Rxh7 i arriba just a temps per jugar 7. ... Rf7 i taules.
Sí, ja ho sé, són finals senzills que la majoria ja hem vist alguna vegada o alguna altra. Però sovint les coses s'obliden, o en una partida real no tenim a ningú al cantó que ens digui: "Mira, aquesta és una posició de problema". Així que com més vegades els veiem, més possibilitats tenim de recordar-nos-en.
Després d'aquests dos finals de peons que eren taules, en veurem dos més amb peons de torre que es guanyen per part de les blanques i un altre que el deixaré com a problema. El primer dels que guanyen les blanques és el següent:
Aquest final s'assembla a l'anterior. El peó d'h7 està perdut. Si les negres aconsegueixen arribar a f7 en el moment en què les blanques es mengin el peó d'h7, seran taules. Les blanques han de lluitar per poder-se menjar el peó, impedint a la vegada que el negre arribi a f7 a temps.
Com abans, el negre intenta agafar la diagonal a2-g8, que li donaria les taules. El blanc li ho impedeix: 1. Rd6 Rf3 2. Re5! única per impedir al negre arribar a temps a la diagonal. Si 2. Re6 Re4 3. Rf6 Rd5 i arriba a la diagonal. 2. ... Re3 3. Rf6 Re4 4. Rg7 Rf5 5. Rxh7 Rf6 6. Rg8 i les blanques guanyen.
Ja per últim, en el següent final, també guanyen les blanques:
Si les blanques intenten 1. h4, no arriben a temps, perquè el negre aconsegueix arribar a temps a la casella f7. Per exemple 1. ... Rd3 2. h5 Re4 3. h6 Rd5 i aconsegueix arribar a la diagonal. Tampoc serveix 3. Rg7 Rf5 4. Rxh7 Rf6 i taules.
Tampoc els serveix a les blanques anar a menjar el peó mitjançant la maniobra Rg5-h6. Per exemple, 1. Rg5 Rd3 2. Rh6 Re4 3. Rxh7 Rf5 i taules.
La solució és jugar 1. Rg7!, que malgrat sembla que perdi temps, ja que el negre pot jugar 1. ... h5, el blanc aconsegueix arribar a temps a g7. 2. Rg6 h4 (si 2. ... Rd3 3. Rxh5 Re4 4. Rg6 i el blanc corona). 3. Rg5 h3 (si 3. ... Rd3 4. Rxh4 Re4 5. Rg5 guanyant) 4. Rg4 Rd3 5. Rxh3 Re4 6. Rg4 i el blanc corona.
Ja per acabar, un problema que no té massa a veure amb els anteriors, excepte que és un final de peons.
A la següent posició, juguen blanques i guanyen:
Sí, realment sembla que les blanques estan molt millor, però no s'han de desestimar les possibilitats defensives derivades de la jugada 1. ... h5.
El deixo com a problema, per si algú se'l vol pensar. No és excessivament difícil, però s'ha d'anar una mica amb compte.

En aquest cas juguen blanques. Les blanques tenen un peó a sisena, mentre que el de les negres està a segona. En principi, això seria bo pel blanc, però si ens mirem una mica millor la posició, veiem que el peó de b6 es perd irremediablement. Si el blanc intenta anar a defensar-lo, 1. Rf4 Rd3 2. Re5 Rc4 3. Rd6 Rb5 4. Rc7, el negre el guanya simplement jugant Ra6.
Així doncs, amb el peó de b6 perdut, el blanc intentarà fer taules. Però, com s'aconsegueixen les taules? Doncs la forma de fer-ho és col.locant-se a b4 just quan el rei negre acabi de menjar el peó de b6. Per tant, l'objectiu del blanc és poder arribar a b4. I quina és la forma més ràpida d'arribar-hi? Doncs, encara que sembli mentida, la forma més ràpida d'arribar-hi és mitjançant les diagonals g3-e1 i e1-b4.
Ja hem vist que amb Rf4 no s'aconseguia arribar a b4 a temps. I què passaria si el blanc jugués 1. Rf3, que en principi està més a prop de b4 que f2? Si el blanc jugués 1. Rf3, el negre podria jugar 1. ... Rd3! tapant el pas del blanc cap a b4.
Així que la única solució és 1. Rf2! Rd3 2. Re1 Rc4 3. Rd2 Rb5 4. Rc3 Rxb6 i arribem a temps a jugar 5. Rb4 taules. Si el negre ens hagués volgut tapar la diagonal jugant 1. ... Rd2, simplement juguem 2. Rf1. A 2. ... Rd3 o Rc3 es contesta 3. Re1, com abans, arribant a temps a b4. A 2. ... Rd1 es contesta 3. Rf2 i també s'arriba a temps a b4.
El següent final és semblant al que acabo d'explicar:

El peó negre d'h7 està perdut. Així doncs, les negres no poden aspirar a res més que a fer taules. Per fer taules, han d'aconseguir portar el seu rei a f7 just en el moment en què les blanques mengin el peó d'a7. Per fer-ho, altra vegada s'ha d'utilitzar una diagonal, en aquest cas la diagonal a2-g8.
Si el negre jugués 1. ... Rc1, perderia i no podria arribar a f7 a temps: 2. Rc3! Rb1 3. Rd4 Rc2 4. Re5 Rd3 5. Rf6 Re4 6. Rg7 Rf5 7. Rxh7 Rf6 8. Rg8.
Però el negre pot aconseguir les taules mitjançant 1. ... Ra1! 2. Rc3 Ra1 3. Rd4 Rb3 4. Re5 Rc4 5. Rf6 Rd5 6. Rg7 Re6 7. Rxh7 i arriba just a temps per jugar 7. ... Rf7 i taules.
Sí, ja ho sé, són finals senzills que la majoria ja hem vist alguna vegada o alguna altra. Però sovint les coses s'obliden, o en una partida real no tenim a ningú al cantó que ens digui: "Mira, aquesta és una posició de problema". Així que com més vegades els veiem, més possibilitats tenim de recordar-nos-en.
Després d'aquests dos finals de peons que eren taules, en veurem dos més amb peons de torre que es guanyen per part de les blanques i un altre que el deixaré com a problema. El primer dels que guanyen les blanques és el següent:

Aquest final s'assembla a l'anterior. El peó d'h7 està perdut. Si les negres aconsegueixen arribar a f7 en el moment en què les blanques es mengin el peó d'h7, seran taules. Les blanques han de lluitar per poder-se menjar el peó, impedint a la vegada que el negre arribi a f7 a temps.
Com abans, el negre intenta agafar la diagonal a2-g8, que li donaria les taules. El blanc li ho impedeix: 1. Rd6 Rf3 2. Re5! única per impedir al negre arribar a temps a la diagonal. Si 2. Re6 Re4 3. Rf6 Rd5 i arriba a la diagonal. 2. ... Re3 3. Rf6 Re4 4. Rg7 Rf5 5. Rxh7 Rf6 6. Rg8 i les blanques guanyen.
Ja per últim, en el següent final, també guanyen les blanques:

Si les blanques intenten 1. h4, no arriben a temps, perquè el negre aconsegueix arribar a temps a la casella f7. Per exemple 1. ... Rd3 2. h5 Re4 3. h6 Rd5 i aconsegueix arribar a la diagonal. Tampoc serveix 3. Rg7 Rf5 4. Rxh7 Rf6 i taules.
Tampoc els serveix a les blanques anar a menjar el peó mitjançant la maniobra Rg5-h6. Per exemple, 1. Rg5 Rd3 2. Rh6 Re4 3. Rxh7 Rf5 i taules.
La solució és jugar 1. Rg7!, que malgrat sembla que perdi temps, ja que el negre pot jugar 1. ... h5, el blanc aconsegueix arribar a temps a g7. 2. Rg6 h4 (si 2. ... Rd3 3. Rxh5 Re4 4. Rg6 i el blanc corona). 3. Rg5 h3 (si 3. ... Rd3 4. Rxh4 Re4 5. Rg5 guanyant) 4. Rg4 Rd3 5. Rxh3 Re4 6. Rg4 i el blanc corona.
Ja per acabar, un problema que no té massa a veure amb els anteriors, excepte que és un final de peons.
A la següent posició, juguen blanques i guanyen:

Sí, realment sembla que les blanques estan molt millor, però no s'han de desestimar les possibilitats defensives derivades de la jugada 1. ... h5.
El deixo com a problema, per si algú se'l vol pensar. No és excessivament difícil, però s'ha d'anar una mica amb compte.
divendres, 16 de setembre del 2005
El problema de la setmana - mat en una
Tal com ja vaig fer fa un temps, aquesta setmana el problema és a la vegada el problema de la setmana del blog i un problema per aconseguir punts per la web d'escaquejant. En concret, jo donaré un punt a tothom qui el resolgui (per la puntuació del problema de la setmana) i s'obtindran 3 punts per la puntuació del problema del mes a escaquejant.
Per tal de no espatllar el problema a la gent que vingui al darrere, agrairia a tothom que no posés la solució com a comentari, per així poder deixar resoldre el problema a més gent millor. La solució me la podeu enviar al correu que hi ha a la columna de la dreta del blog. Si a algú no li interessen els punts d'escaquejant o els punts d'aquí, que m'ho faci saber i no l'inclouré a la llista. Qualsevol dubte es pot posar com a comentari (no cal registrar-se ni res).
El diumenge que ve (dia 25 de setembre) posaré la solució, les persones que l'han resolt i enviaré la llista de la gent que ho ha resolt a l'escaquejant.
I, ara ja sí, el problema:
En la posició següent:
Per tal de no espatllar el problema a la gent que vingui al darrere, agrairia a tothom que no posés la solució com a comentari, per així poder deixar resoldre el problema a més gent millor. La solució me la podeu enviar al correu que hi ha a la columna de la dreta del blog. Si a algú no li interessen els punts d'escaquejant o els punts d'aquí, que m'ho faci saber i no l'inclouré a la llista. Qualsevol dubte es pot posar com a comentari (no cal registrar-se ni res).
El diumenge que ve (dia 25 de setembre) posaré la solució, les persones que l'han resolt i enviaré la llista de la gent que ho ha resolt a l'escaquejant.
I, ara ja sí, el problema:
En la posició següent:
les blanques juguen i fan mat en una jugada.
Observació: un cop vist com es fa mat en una, hi ha dues solucions al problema. Perquè el problema sigui vàlid, s'han de donar les dues solucions.
Setmana anterior
Setmana següent
diumenge, 11 de setembre del 2005
divendres, 9 de setembre del 2005
Problema d'escacs
Juguen blanques i guanyen:
No és excessivament difícil, però és maco.
I ja que poso un problema nou, aprofito per posar les solucions al problema del 29 d'agost i a l'estudi, que s'han quedat per aquí sense resoldre.

No és excessivament difícil, però és maco.
I ja que poso un problema nou, aprofito per posar les solucions al problema del 29 d'agost i a l'estudi, que s'han quedat per aquí sense resoldre.
El problema de la setmana - 65
El problema d'aquesta setmana consisteix a afegir 5 signes de suma o resta a la següent seqüència de números:
123456789
per obtenir el número 65.
De la mateixa manera, també afegir 5 signes de suma o resta a la seqüència
987654321
per obtenir també el número 65.
Si per exemple s'hagués d'obtenir el número 100, amb els 5 signes de suma o resta, es podria aconseguir:
9-8+76+54-32+1.
Setmana anterior
Setmana següent
123456789
per obtenir el número 65.
De la mateixa manera, també afegir 5 signes de suma o resta a la seqüència
987654321
per obtenir també el número 65.
Si per exemple s'hagués d'obtenir el número 100, amb els 5 signes de suma o resta, es podria aconseguir:
9-8+76+54-32+1.
Setmana anterior
Setmana següent
dissabte, 3 de setembre del 2005
El problema de la setmana - El menor número
Quin és el número més petit que, quan es divideix per 2, dóna de residu 1; quan es divideix per 3, dóna de residu 2; quan es divideix per 4, dóna de residu 3; per 5, dóna 4; per 6, 5; per 7, 5; per 8, 7 i per 9, 8?
Setmana anterior
Setmana següent
Setmana anterior
Setmana següent
dijous, 1 de setembre del 2005
Estudis
Després de penjar un problema diari durant un mes, ara tenia una mica de mono de penjar i resoldre problemes. Així que en penjo un altre. Està tret de la pàgina d'estudis de finals de ChessCafe.com, on cada setmana publiquen un estudi.
En aquest cas, les blanques juguen i fan taules:
Dels problemes de l'agost, per si algú s'hi vol entretenir, encara queden el del 26 d'agost (que em sembla que també entra dins la categoria d'estudis de finals) i la "brometa" del 21 d'agost, que està gairebé resolta, només falten les jugades concretes.
De fet, també falta per resoldre el problema del 29 d'agost (que me n'havia descuidat).
En aquest cas, les blanques juguen i fan taules:

Dels problemes de l'agost, per si algú s'hi vol entretenir, encara queden el del 26 d'agost (que em sembla que també entra dins la categoria d'estudis de finals) i la "brometa" del 21 d'agost, que està gairebé resolta, només falten les jugades concretes.
De fet, també falta per resoldre el problema del 29 d'agost (que me n'havia descuidat).
dimecres, 31 d’agost del 2005
Simultànies amb en Viktor Kortchnoi
El passat 22 d'agost i organitzat pel club d'escacs Banyoles es van jugar unes simultànies amb en Viktor Kortchnoi.
He d'agrair al club d'escacs Banyoles la possibilitat que ens va donar de poder jugar amb en Viktor Kortchnoi. Malgrat pagar 60 euros per poder jugar, va valer la pena. A més, vaig tornar a casa amb el tauler en el que vaig jugar signat per en Kortchnoi, la planilla (també signada per en Kortchnoi i que un dia d'aquests quedarà emmarcada) i les peces amb les que vaig guanyar (privilegi que només se'ns va concedir a les 3 persones que vam aconseguir la victòria).
No tenia intenció de posar la partida, però ja que dues persones m'ho van demanar, la posaré. De fet, aquestes dues persones són gairebé les que van començar a donar vida a aquest blog quan feia un munt de temps que jo estava escrivint aquí i només hi entrava jo i de tant en tant algú altre. Així que si em demanen que posi la partida, jo la poso.
Les fotos que surten aquí són de l'Albert Badosa, que es va passar el matí fent-nos fotos i vídeos i que després, molt amablement, ens va passar un cd amb les fotos i els vídeos, que quedarà guardat molt a prop de la planilla, el tauler i tota la resta. "El santuari d'en Kortchnoi", que em va dir un company de club.
Anem per la partida. Una altra de les coses amb les que ens va obsequiar el club d'escacs Banyoles va ser amb un foli, on a la part de baix hi havia el següent:
Abans de començar la partida estava sense el resultat, és clar, i servia perquè en Kortchnoi sabés amb qui jugava. Un cop acabada la partida, el foli tenia l'espai suficient a dalt per posar-hi la planilla (que es pot trobar escanejada al final del post) i que, òbviament, serà part del que s'emmarqui un dia d'aquests.
1. d4
Algú m'havia suggerit que no jugués una francesa, perquè en Kortchnoi n'és un especialista. Jo estava segura de jugar una francesa en cas de que ell em sortís d'e4. Què hauria de jugar, sinó? Si no m'equivoco, i després d'un temps en què a 1. e4 contestava e5, porto uns 15 anys jugant la francesa. No sé jugar res més. Per què hauria de canviar? Sí, ja sé que en Kortchnoi l'ha jugat molts més anys que jo, però no era qüestió de canviar d'obertura així perquè sí. Si m'ha de massacrar, almenys que n'aprengui alguna cosa i no faci el mateix en una partida de campionat.
Així que la resposta a d4 estava cantada. Si s'atreveix, perfecte :-)
1. ... e6
2. e4 d5
3. Cc3 dxe4
4. Cxe4 Cd7
5. Cf3 Cgf6
Si no m'equivoco, aquesta foto està feta just en aquest moment de la partida.
6. Cxf6+ Cxf6
7. c3 Ae7
8. Ae3 0-0
9. Ad3 b6
10. Dc2 Ab7
11. Ce5 c5
12. 0-0-0 Dc7
13. f4 Tfd8
14. The1 cxd4
15. Axd4 Ac5
16. Axc5 Dxc5
17. g4
He de reconèixer que, arribat aquest punt, em pensava que em faria algun mat d'aquells ràpids i vaig començar a mirar al meu voltant, a veure si acabava alguna partida, que no volia ser la primera a perdre (visca l'optimisme!) La cosa no té massa bona pinta i sembla que g6 és obligada.
17. ... g6
18. f5
Malgrat que em feia por que em sacrifiqués el cavall a f7, aquí em vaig decidir per Td5. Si no sacrificava a f7, li treia el cavall del mig. I si sacrificava... doncs també. Tot i que no les tenia pas totes.
18. ... Td5
19. Cxf7
Un cop perpretat el sacrifici, sembla que me l'he de menjar. I que passi el que hagi de passar.
19. ... Rxf7
Seguia pensant que em mataria ràpid. Pensava que em menjaria el peó d'e6 o el de g6 i el meu rei es quedaria del tot desprotegit. Però em va sorprendre:
20. g5
Aquí vaig pensar a marxar amb el cavall. Però, on podia anar? No m'agradava cap quadre. Així que vaig pensar que tenia peça de més, així que li podia tornar tranquil.lament una peça. A sobre, em quedava amb peó de més. Així que em vaig decidir: em quedo amb peó de més i el rei una mica desprotegit, però si aconsegueixo parar l'atac que em pugui fer, un peó sempre serà un peó.
20. ... exf5
21. gxf6 Rxf6
22. Dd2 Tad8
23. Dh6
Em fa aquesta jugada i el primer que penso és: "No pot ser que s'hagi deixat l'àlfil". I, efectivament, aquest àlfil no me'l puc menjar. A 23. ... Txd3 24. Txd3 Txd3 25. Dh4+. A Rg7 segueix Te7+ i a Rf7, segueix Dh7+. Així que s'ha de defensar el peó d'h7 i la casella e7. No tinc gaires opcions.
23. ... T5d7
24. Dh4+ Rg7
25. Te6
Altre cop no em puc menjar l'àlfil de d3 per Te7+. Per no tenir problemes, em va semblar que el més sensat era defensar la casella f6 i preveient el seu Tde1, em va semblar que ho podria fer fàcilment amb Tf8 i llavors tencar-me en banda portant la torre a f7. I així ho vaig fer:
25. ... Tf8
26. Tde1 Tff7
27. Ac2
Un cop he aconseguit parar l'atac, ara el que cal és canviar peces, que per alguna cosa tinc peó de més. El primer que vull canviar és la dama, no fos cas que encara revifés l'atac. Així que ho intento amb la maniobra Ad5-Dc4.
27. ... Ad5
28. T6e5 Dc4
29. Dxc4 Axc4
30. b3 Ad3
Arribat a aquest moment, jo li jugo Ad3 i em diu alguna cosa. Jo no l'entenc. De cop, veig que el meu tauler s'omple de gent que ve a mirar què ha passat. I pel que diu la gent, dedueixo que ha abandonat. Intento escriure la jugada i el boli em falla. Una estona més tard algú em diu que em va dir "usted gana". Ja podria ser, ja, però jo no me'n vaig enterar.
A la següent volta va signar la planilla (fins que no va signar jo no m'acabava de creure que hagués abandonat). I això és tot.
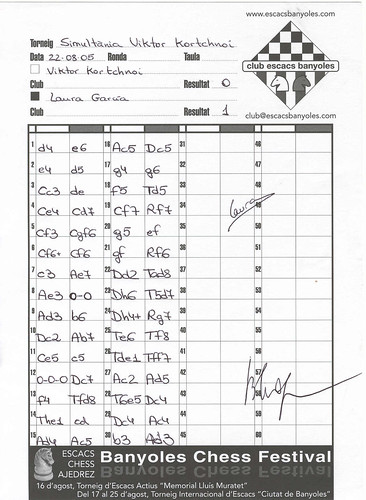
I, ja per acabar, la planilla. En ella s'hi pot observar la meva fabulosa lletra :-) També s'hi pot observar com la última jugada està feta amb un pols lleugerament més tremolós. Si a algú li interessa, clicant sobre ella, es veu la foto amb més ressolució.
Clicant aquí es pot trobar una altra versió del que van ser les simultànies, amb tros d'una altra partida.

He d'agrair al club d'escacs Banyoles la possibilitat que ens va donar de poder jugar amb en Viktor Kortchnoi. Malgrat pagar 60 euros per poder jugar, va valer la pena. A més, vaig tornar a casa amb el tauler en el que vaig jugar signat per en Kortchnoi, la planilla (també signada per en Kortchnoi i que un dia d'aquests quedarà emmarcada) i les peces amb les que vaig guanyar (privilegi que només se'ns va concedir a les 3 persones que vam aconseguir la victòria).
No tenia intenció de posar la partida, però ja que dues persones m'ho van demanar, la posaré. De fet, aquestes dues persones són gairebé les que van començar a donar vida a aquest blog quan feia un munt de temps que jo estava escrivint aquí i només hi entrava jo i de tant en tant algú altre. Així que si em demanen que posi la partida, jo la poso.
Les fotos que surten aquí són de l'Albert Badosa, que es va passar el matí fent-nos fotos i vídeos i que després, molt amablement, ens va passar un cd amb les fotos i els vídeos, que quedarà guardat molt a prop de la planilla, el tauler i tota la resta. "El santuari d'en Kortchnoi", que em va dir un company de club.

Anem per la partida. Una altra de les coses amb les que ens va obsequiar el club d'escacs Banyoles va ser amb un foli, on a la part de baix hi havia el següent:

Abans de començar la partida estava sense el resultat, és clar, i servia perquè en Kortchnoi sabés amb qui jugava. Un cop acabada la partida, el foli tenia l'espai suficient a dalt per posar-hi la planilla (que es pot trobar escanejada al final del post) i que, òbviament, serà part del que s'emmarqui un dia d'aquests.
1. d4
Algú m'havia suggerit que no jugués una francesa, perquè en Kortchnoi n'és un especialista. Jo estava segura de jugar una francesa en cas de que ell em sortís d'e4. Què hauria de jugar, sinó? Si no m'equivoco, i després d'un temps en què a 1. e4 contestava e5, porto uns 15 anys jugant la francesa. No sé jugar res més. Per què hauria de canviar? Sí, ja sé que en Kortchnoi l'ha jugat molts més anys que jo, però no era qüestió de canviar d'obertura així perquè sí. Si m'ha de massacrar, almenys que n'aprengui alguna cosa i no faci el mateix en una partida de campionat.
Així que la resposta a d4 estava cantada. Si s'atreveix, perfecte :-)
1. ... e6
2. e4 d5
3. Cc3 dxe4
4. Cxe4 Cd7
5. Cf3 Cgf6

Si no m'equivoco, aquesta foto està feta just en aquest moment de la partida.
6. Cxf6+ Cxf6
7. c3 Ae7
8. Ae3 0-0
9. Ad3 b6
10. Dc2 Ab7
11. Ce5 c5
12. 0-0-0 Dc7
13. f4 Tfd8
14. The1 cxd4
15. Axd4 Ac5
16. Axc5 Dxc5
17. g4

He de reconèixer que, arribat aquest punt, em pensava que em faria algun mat d'aquells ràpids i vaig començar a mirar al meu voltant, a veure si acabava alguna partida, que no volia ser la primera a perdre (visca l'optimisme!) La cosa no té massa bona pinta i sembla que g6 és obligada.
17. ... g6
18. f5
Malgrat que em feia por que em sacrifiqués el cavall a f7, aquí em vaig decidir per Td5. Si no sacrificava a f7, li treia el cavall del mig. I si sacrificava... doncs també. Tot i que no les tenia pas totes.
18. ... Td5
19. Cxf7

Un cop perpretat el sacrifici, sembla que me l'he de menjar. I que passi el que hagi de passar.
19. ... Rxf7
Seguia pensant que em mataria ràpid. Pensava que em menjaria el peó d'e6 o el de g6 i el meu rei es quedaria del tot desprotegit. Però em va sorprendre:
20. g5

Aquí vaig pensar a marxar amb el cavall. Però, on podia anar? No m'agradava cap quadre. Així que vaig pensar que tenia peça de més, així que li podia tornar tranquil.lament una peça. A sobre, em quedava amb peó de més. Així que em vaig decidir: em quedo amb peó de més i el rei una mica desprotegit, però si aconsegueixo parar l'atac que em pugui fer, un peó sempre serà un peó.
20. ... exf5
21. gxf6 Rxf6
22. Dd2 Tad8
23. Dh6

Em fa aquesta jugada i el primer que penso és: "No pot ser que s'hagi deixat l'àlfil". I, efectivament, aquest àlfil no me'l puc menjar. A 23. ... Txd3 24. Txd3 Txd3 25. Dh4+. A Rg7 segueix Te7+ i a Rf7, segueix Dh7+. Així que s'ha de defensar el peó d'h7 i la casella e7. No tinc gaires opcions.
23. ... T5d7
24. Dh4+ Rg7
25. Te6

Altre cop no em puc menjar l'àlfil de d3 per Te7+. Per no tenir problemes, em va semblar que el més sensat era defensar la casella f6 i preveient el seu Tde1, em va semblar que ho podria fer fàcilment amb Tf8 i llavors tencar-me en banda portant la torre a f7. I així ho vaig fer:
25. ... Tf8
26. Tde1 Tff7
27. Ac2
Un cop he aconseguit parar l'atac, ara el que cal és canviar peces, que per alguna cosa tinc peó de més. El primer que vull canviar és la dama, no fos cas que encara revifés l'atac. Així que ho intento amb la maniobra Ad5-Dc4.
27. ... Ad5
28. T6e5 Dc4
29. Dxc4 Axc4
30. b3 Ad3

Arribat a aquest moment, jo li jugo Ad3 i em diu alguna cosa. Jo no l'entenc. De cop, veig que el meu tauler s'omple de gent que ve a mirar què ha passat. I pel que diu la gent, dedueixo que ha abandonat. Intento escriure la jugada i el boli em falla. Una estona més tard algú em diu que em va dir "usted gana". Ja podria ser, ja, però jo no me'n vaig enterar.
A la següent volta va signar la planilla (fins que no va signar jo no m'acabava de creure que hagués abandonat). I això és tot.
I, ja per acabar, la planilla. En ella s'hi pot observar la meva fabulosa lletra :-) També s'hi pot observar com la última jugada està feta amb un pols lleugerament més tremolós. Si a algú li interessa, clicant sobre ella, es veu la foto amb més ressolució.
Clicant aquí es pot trobar una altra versió del que van ser les simultànies, amb tros d'una altra partida.
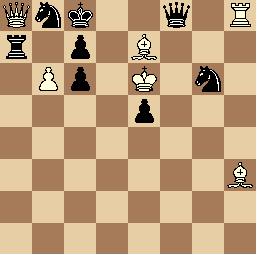
Problema d'escacs - 31 agost
Juguen negres i guanyen:
I amb aquest problema s'acaben els problemes diaris del mes d'agost. Potser algun altre dia en poso algun altre.

I amb aquest problema s'acaben els problemes diaris del mes d'agost. Potser algun altre dia en poso algun altre.
dimarts, 30 d’agost del 2005
dilluns, 29 d’agost del 2005
diumenge, 28 d’agost del 2005
dissabte, 27 d’agost del 2005
El problema de la setmana - Un altre criptograma
Com que aquesta setmana ja arriba el setembre, el problema de la setmana torna al seu funcionament normal: cada dissabte/diumenge hi haurà un problema nou.
Aquest cop, torna a tocar un altre criptograma, també de l'Alan Wayne. Aquest criptograma compleix les propietats que el director de la revista American Mathematical Monthly considera "encantadores" per un criptograma:
- Les lletres formen paraules (en anglès).
- S'utilitzen tots els dígits.
- La solució és única.
- Es resol per lògica, no tantejant.
El criptograma en qüestió és el següent:
FORTY + TEN + TEN = SIXTY
Prometo no posar cap més criptograma en un cert temps.
Setmana anterior
Setmana següent
Aquest cop, torna a tocar un altre criptograma, també de l'Alan Wayne. Aquest criptograma compleix les propietats que el director de la revista American Mathematical Monthly considera "encantadores" per un criptograma:
- Les lletres formen paraules (en anglès).
- S'utilitzen tots els dígits.
- La solució és única.
- Es resol per lògica, no tantejant.
El criptograma en qüestió és el següent:
FORTY + TEN + TEN = SIXTY
Prometo no posar cap més criptograma en un cert temps.
Setmana anterior
Setmana següent
SIX+SIX+SIX = NINE+NINE
El problema de la setmana anterior consistia a trobar per quin número s'havia de substituir cadascuna de les lletres perquè la igualtat anterior fos certa.
La única solució que no conté números que comencin per 0 és la que molt bé ha trobat en pacopat:
942 + 942 + 942 = 1413 + 1413.
Deia que aquí es podien trobar referències al número pi. La primera, i que es veu més a simple vista, és la del número 1413, que llegit al revés conté les 4 primeres xifres del número pi (sense arrodonir, però no es pot pas tenir tot!)
Una segona relació es troba amb el número 942. En aquest cas, el número 942 està multiplicat per 3. Si el dividim per 3 ens dóna 314, que són les 3 primeres xifres del número pi.
Que està molt agafat pels pèls? Potser sí, però es pot seguir. Si admetem que un número pugui començar per zero, el criptograma té una altra solució:
472 + 472 + 472 = 0708 + 0708.
En aquest cas, si sumem el que tenim a cada banda de la igualtat, obtenim el número 1416, que són els decimals de pi que tots coneixem (ara sí, arrodonint).
I ja per acabar, gairebé trobem una altra relació: 472 = 314 + 158. Si en comptes de tenir el 472 tinguessim el 473, tindríem 314 + 159, que conté les xifres de pi: 3.14159.
Casualitats? Massa poca feina? Com a mínim és curiós.
La única solució que no conté números que comencin per 0 és la que molt bé ha trobat en pacopat:
942 + 942 + 942 = 1413 + 1413.
Deia que aquí es podien trobar referències al número pi. La primera, i que es veu més a simple vista, és la del número 1413, que llegit al revés conté les 4 primeres xifres del número pi (sense arrodonir, però no es pot pas tenir tot!)
Una segona relació es troba amb el número 942. En aquest cas, el número 942 està multiplicat per 3. Si el dividim per 3 ens dóna 314, que són les 3 primeres xifres del número pi.
Que està molt agafat pels pèls? Potser sí, però es pot seguir. Si admetem que un número pugui començar per zero, el criptograma té una altra solució:
472 + 472 + 472 = 0708 + 0708.
En aquest cas, si sumem el que tenim a cada banda de la igualtat, obtenim el número 1416, que són els decimals de pi que tots coneixem (ara sí, arrodonint).
I ja per acabar, gairebé trobem una altra relació: 472 = 314 + 158. Si en comptes de tenir el 472 tinguessim el 473, tindríem 314 + 159, que conté les xifres de pi: 3.14159.
Casualitats? Massa poca feina? Com a mínim és curiós.
divendres, 26 d’agost del 2005
dijous, 25 d’agost del 2005
dimecres, 24 d’agost del 2005
dimarts, 23 d’agost del 2005
dilluns, 22 d’agost del 2005
diumenge, 21 d’agost del 2005
El problema de la setmana - 6+6+6=9+9
El problema d'aquesta setmana està tret de Los mágicos números del Doctor Matrix, d'en Martin Gardner. Ha caigut avui a les meves mans i no m'he pogut estar de fullejar-lo bastant exhaustivament i he trobat un bonic problema (i més que n'hi trobaré).
Es tracta del següent criptograma:
SIX + SIX + SIX = NINE + NINE
A cada lletra li correspon un número diferent. El problema (facilet) es tracta només de trobar quin número correspon a cada lletra. Si no s'admeten números que comencin amb 0, la solució és única. Si es permeten números que comencin amb 0, hi ha una altra solució.
El curiós del tema (que no és el problema de la setmana), és que a la primera solució (la que no permet números que comencin amb 0) contè una relació amb el número pi de dues formes diferents. Però la cosa no acaba aquí, perquè amb la solució que permet números que comencen per 0, també hi ha una relació amb pi.
Setmana anterior
Setmana següent
Es tracta del següent criptograma:
SIX + SIX + SIX = NINE + NINE
A cada lletra li correspon un número diferent. El problema (facilet) es tracta només de trobar quin número correspon a cada lletra. Si no s'admeten números que comencin amb 0, la solució és única. Si es permeten números que comencin amb 0, hi ha una altra solució.
El curiós del tema (que no és el problema de la setmana), és que a la primera solució (la que no permet números que comencin amb 0) contè una relació amb el número pi de dues formes diferents. Però la cosa no acaba aquí, perquè amb la solució que permet números que comencen per 0, també hi ha una relació amb pi.
Setmana anterior
Setmana següent
dissabte, 20 d’agost del 2005
divendres, 19 d’agost del 2005
dijous, 18 d’agost del 2005
Subscriure's a:
Comentaris (Atom)