Simultànies amb en Viktor Kortchnoi

El passat 22 d'agost i organitzat pel club d'escacs Banyoles es van jugar unes simultànies amb en Viktor Kortchnoi.

He d'agrair al club d'escacs Banyoles la possibilitat que ens va donar de poder jugar amb en Viktor Kortchnoi. Malgrat pagar 60 euros per poder jugar, va valer la pena. A més, vaig tornar a casa amb el tauler en el que vaig jugar signat per en Kortchnoi, la planilla (també signada per en Kortchnoi i que un dia d'aquests quedarà emmarcada) i les peces amb les que vaig guanyar (privilegi que només se'ns va concedir a les 3 persones que vam aconseguir la victòria).

No tenia intenció de posar la partida, però ja que dues persones m'ho van demanar, la posaré. De fet, aquestes dues persones són gairebé les que van començar a donar vida a aquest blog quan feia un munt de temps que jo estava escrivint aquí i només hi entrava jo i de tant en tant algú altre. Així que si em demanen que posi la partida, jo la poso.

Les fotos que surten aquí són de l'Albert Badosa, que es va passar el matí fent-nos fotos i vídeos i que després, molt amablement, ens va passar un cd amb les fotos i els vídeos, que quedarà guardat molt a prop de la planilla, el tauler i tota la resta. "El santuari d'en Kortchnoi", que em va dir un company de club.

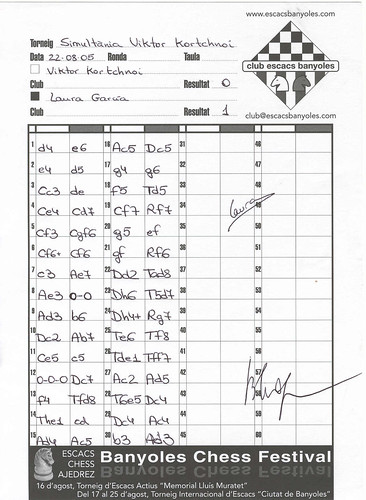
Anem per la partida. Una altra de les coses amb les que ens va obsequiar el club d'escacs Banyoles va ser amb un foli, on a la part de baix hi havia el següent:

Abans de començar la partida estava sense el resultat, és clar, i servia perquè en Kortchnoi sabés amb qui jugava. Un cop acabada la partida, el foli tenia l'espai suficient a dalt per posar-hi la planilla (que es pot trobar escanejada al final del post) i que, òbviament, serà part del que s'emmarqui un dia d'aquests.

1. d4

Algú m'havia suggerit que no jugués una francesa, perquè en Kortchnoi n'és un especialista. Jo estava segura de jugar una francesa en cas de que ell em sortís d'e4. Què hauria de jugar, sinó? Si no m'equivoco, i després d'un temps en què a 1. e4 contestava e5, porto uns 15 anys jugant la francesa. No sé jugar res més. Per què hauria de canviar? Sí, ja sé que en Kortchnoi l'ha jugat molts més anys que jo, però no era qüestió de canviar d'obertura així perquè sí. Si m'ha de massacrar, almenys que n'aprengui alguna cosa i no faci el mateix en una partida de campionat.

Així que la resposta a d4 estava cantada. Si s'atreveix, perfecte :-)

1. ... e6
2. e4 d5
3. Cc3 dxe4
4. Cxe4 Cd7
5. Cf3 Cgf6

Si no m'equivoco, aquesta foto està feta just en aquest moment de la partida.

6. Cxf6+ Cxf6
7. c3 Ae7
8. Ae3 0-0
9. Ad3 b6
10. Dc2 Ab7
11. Ce5 c5
12. 0-0-0 Dc7
13. f4 Tfd8
14. The1 cxd4
15. Axd4 Ac5
16. Axc5 Dxc5
17. g4

He de reconèixer que, arribat aquest punt, em pensava que em faria algun mat d'aquells ràpids i vaig començar a mirar al meu voltant, a veure si acabava alguna partida, que no volia ser la primera a perdre (visca l'optimisme!) La cosa no té massa bona pinta i sembla que g6 és obligada.

17. ... g6
18. f5

Malgrat que em feia por que em sacrifiqués el cavall a f7, aquí em vaig decidir per Td5. Si no sacrificava a f7, li treia el cavall del mig. I si sacrificava... doncs també. Tot i que no les tenia pas totes.

18. ... Td5
19. Cxf7

Un cop perpretat el sacrifici, sembla que me l'he de menjar. I que passi el que hagi de passar.

19. ... Rxf7

Seguia pensant que em mataria ràpid. Pensava que em menjaria el peó d'e6 o el de g6 i el meu rei es quedaria del tot desprotegit. Però em va sorprendre:

20. g5

Aquí vaig pensar a marxar amb el cavall. Però, on podia anar? No m'agradava cap quadre. Així que vaig pensar que tenia peça de més, així que li podia tornar tranquil.lament una peça. A sobre, em quedava amb peó de més. Així que em vaig decidir: em quedo amb peó de més i el rei una mica desprotegit, però si aconsegueixo parar l'atac que em pugui fer, un peó sempre serà un peó.

20. ... exf5
21. gxf6 Rxf6
22. Dd2 Tad8
23. Dh6

Em fa aquesta jugada i el primer que penso és: "No pot ser que s'hagi deixat l'àlfil". I, efectivament, aquest àlfil no me'l puc menjar. A 23. ... Txd3 24. Txd3 Txd3 25. Dh4+. A Rg7 segueix Te7+ i a Rf7, segueix Dh7+. Així que s'ha de defensar el peó d'h7 i la casella e7. No tinc gaires opcions.

23. ... T5d7
24. Dh4+ Rg7
25. Te6

Altre cop no em puc menjar l'àlfil de d3 per Te7+. Per no tenir problemes, em va semblar que el més sensat era defensar la casella f6 i preveient el seu Tde1, em va semblar que ho podria fer fàcilment amb Tf8 i llavors tencar-me en banda portant la torre a f7. I així ho vaig fer:

25. ... Tf8
26. Tde1 Tff7
27. Ac2

Un cop he aconseguit parar l'atac, ara el que cal és canviar peces, que per alguna cosa tinc peó de més. El primer que vull canviar és la dama, no fos cas que encara revifés l'atac. Així que ho intento amb la maniobra Ad5-Dc4.

27. ... Ad5
28. T6e5 Dc4
29. Dxc4 Axc4
30. b3 Ad3

Arribat a aquest moment, jo li jugo Ad3 i em diu alguna cosa. Jo no l'entenc. De cop, veig que el meu tauler s'omple de gent que ve a mirar què ha passat. I pel que diu la gent, dedueixo que ha abandonat. Intento escriure la jugada i el boli em falla. Una estona més tard algú em diu que em va dir "usted gana". Ja podria ser, ja, però jo no me'n vaig enterar.

A la següent volta va signar la planilla (fins que no va signar jo no m'acabava de creure que hagués abandonat). I això és tot.


I, ja per acabar, la planilla. En ella s'hi pot observar la meva fabulosa lletra :-) També s'hi pot observar com la última jugada està feta amb un pols lleugerament més tremolós. Si a algú li interessa, clicant sobre ella, es veu la foto amb més ressolució.

Clicant aquí es pot trobar una altra versió del que van ser les simultànies, amb tros d'una altra partida.

Problema d'escacs - 31 agost

Juguen negres i guanyen:

I amb aquest problema s'acaben els problemes diaris del mes d'agost. Potser algun altre dia en poso algun altre.

Problema d'escacs - 30 agost

Juguen negres i fan taules (fàcil, fàcil):

Problema d'escacs - 29 agost

Juguen blanques i guanyen:

Problema d'escacs - 28 agost

Juguen blanques i guanyen:

El problema de la setmana - Un altre criptograma

Com que aquesta setmana ja arriba el setembre, el problema de la setmana torna al seu funcionament normal: cada dissabte/diumenge hi haurà un problema nou.

Aquest cop, torna a tocar un altre criptograma, també de l'Alan Wayne. Aquest criptograma compleix les propietats que el director de la revista American Mathematical Monthly considera "encantadores" per un criptograma:

- Les lletres formen paraules (en anglès).
- S'utilitzen tots els dígits.
- La solució és única.
- Es resol per lògica, no tantejant.

El criptograma en qüestió és el següent:

FORTY + TEN + TEN = SIXTY

Prometo no posar cap més criptograma en un cert temps.


Setmana anterior

Setmana següent

SIX+SIX+SIX = NINE+NINE

El problema de la setmana anterior consistia a trobar per quin número s'havia de substituir cadascuna de les lletres perquè la igualtat anterior fos certa.

La única solució que no conté números que comencin per 0 és la que molt bé ha trobat en pacopat:

942 + 942 + 942 = 1413 + 1413.

Deia que aquí es podien trobar referències al número pi. La primera, i que es veu més a simple vista, és la del número 1413, que llegit al revés conté les 4 primeres xifres del número pi (sense arrodonir, però no es pot pas tenir tot!)

Una segona relació es troba amb el número 942. En aquest cas, el número 942 està multiplicat per 3. Si el dividim per 3 ens dóna 314, que són les 3 primeres xifres del número pi.

Que està molt agafat pels pèls? Potser sí, però es pot seguir. Si admetem que un número pugui començar per zero, el criptograma té una altra solució:

472 + 472 + 472 = 0708 + 0708.

En aquest cas, si sumem el que tenim a cada banda de la igualtat, obtenim el número 1416, que són els decimals de pi que tots coneixem (ara sí, arrodonint).

I ja per acabar, gairebé trobem una altra relació: 472 = 314 + 158. Si en comptes de tenir el 472 tinguessim el 473, tindríem 314 + 159, que conté les xifres de pi: 3.14159.

Casualitats? Massa poca feina? Com a mínim és curiós.

Problema d'escacs - 27 agost

Juguen blanques i guanyen:

Problema d'escacs - 26 agost

Juguen blanques i guanyen:

Problema d'escacs - 25 agost

Juguen blanques i guanyen:

Problema d'escacs - 24 agost

Juguen blanques i guanyen:

Problema d'escacs - 23 agost

Juguen negres i guanyen:

Problema d'escacs - 22 agost

Juguen blanques i guanyen:

El problema de la setmana - 6+6+6=9+9

El problema d'aquesta setmana està tret de Los mágicos números del Doctor Matrix, d'en Martin Gardner. Ha caigut avui a les meves mans i no m'he pogut estar de fullejar-lo bastant exhaustivament i he trobat un bonic problema (i més que n'hi trobaré).

Es tracta del següent criptograma:

SIX + SIX + SIX = NINE + NINE

A cada lletra li correspon un número diferent. El problema (facilet) es tracta només de trobar quin número correspon a cada lletra. Si no s'admeten números que comencin amb 0, la solució és única. Si es permeten números que comencin amb 0, hi ha una altra solució.

El curiós del tema (que no és el problema de la setmana), és que a la primera solució (la que no permet números que comencin amb 0) contè una relació amb el número pi de dues formes diferents. Però la cosa no acaba aquí, perquè amb la solució que permet números que comencen per 0, també hi ha una relació amb pi.

Setmana anterior

Setmana següent

Problema d'escacs - 21 agost

Juguen negres i fan mat en 3:

Problema d'escacs - 20 agost

Juguen blanques i guanyen:

Problema d'escacs - 19 agost

Juguen blanques i guanyen:

Problema d'escacs - 18 agost

Juguen blanques i guanyen:

El problema de la setmana - les 3 bessones

Tenim 3 bessones indistingibles: l'Anna, la Bàrbara i la Carme. L'Anna tant pot dir una mentida com una veritat, la Bàrbara sempre diu la veritat i la Carme sempre menteix. En aquests moments, estan assegudes les 3 de cantó. Una està asseguda a l'esquerra (E), una al mig (M) i una a la dreta (D). Les 3 bessones mantenen la següent conversa:

E a M: Ets una mentidera!
M: No ho sóc!
D: Totes dues sou mentideres.
E: Això és mentida!
M: Això és mentida!
D: Això és mentida!

Es tracta de saber qui és qui.


Setmana anterior

Setmana següent

Problema d'escacs - 17 agost

Juguen negres i guanyen:

(És probable que a algú li soni la posició. A mi em sonava i tinc molt mala memòria)

Problema d'escacs - 16 agost

Juguen blanques i guanyen:

Problema d'escacs - 15 agost

Juguen blanques i guanyen:

(Avís: No és tan senzill com podria semblar. Almenys, a mi no m'ho sembla)

Problema d'escacs - 14 agost

Juguen blanques i guanyen:

El problema de la setmana - dos números

Dos persones estan parlant:

- Estic pensant en un número més petit que 100.
- Jo també.

Una persona li diu el número que ha pensat a l'altra.

- T'has fixat que si sumem el número que has pensat tu i el número que he pensat jo i elevem el resultat al quadrat obtenim un número de quatre dígits, en el que els dos primers dígits són el número que has pensat tu i els altres dos el número que he pensat jo?
- Sí, tens raó, com si haguéssim pensat en el 30 i el 25, que si els sumem ens dóna 55 i si elevem el 55 al quadrat ens dóna 3025.
- Exactament. Només que els números que hem pensat no són ni 30 ni 25.

Quins són els números?

Setmana anterior

Setmana següent

Problema d'escacs - 13 agost

Juguen blanques i guanyen: (tornem als problemes facilets, per cel.lebrar que és cap de setmana)

Problema d'escacs - 12 agost

Juguen blanques i guanyen:

El problema de la setmana - sacs

Tinc 5 sacs de patates i volem saber quant pesa cadascun. El problema és que no tenim cap balança. Però algú que els ha pesat anteriorment ens informa que:

- Els sacs 1 i 2 pesen en conjunt 12 Kg.
- Els sacs 2 i 3 pesen 13.5 Kg entre els dos.
- Els 3 i 4 pesen 11.5 Kg.
- Els 4 i 5, 8 Kg.
- Els sacs 1,3 i 5 pesen 16 Kg entre els tres.

Quant pesa cada sac?

Setmana anterior

Setmana següent

Problema d'escacs - 11 agost

Juguen blanques:

Problema d'escacs - 10 agost

Juguen blanques i guanyen:

Problema d'escacs - 9 agost

Juguen blanques i guanyen:

Arrels complexes visibles

Això està tret de la pàgina Mudd Math Fun Facts, on hi ha diferents coses interessants per ensenyar als alumnes, que no s'avorreixin i s'interessin una mica.

En aquest cas, es tracta de les arrels complexes de les paràboles, com localitzar-les gràficament un cop es té la paràbola dibuixada. Com molt bé explica aquí, el que s'ha de fer és fer la simetria de la paràbola respecte del vèrtex i trobar els punts de tall d'aquesta nova paràbola amb l'eix de les X. Amb aquests dos punts, construir una circumferència on els dos punts siguin els extrems d'un diàmetre (i, per tant, la circumferència està centrada en el punt de l'eix de les X on hi ha el vèrtex de la paràbola). Aleshores, les dues arrels complexes (mirant ara el pla com si fos el pla complex) són els punts de la circumferència que tenen per component x la mateixa que el centre de la circumferència (o la del vèrtex de la paràbola).

La raó? Qualsevol paràbola es pot posar com y=k(x-a)^2+b. N'hi ha prou a desenvolupar això per veure-ho: kx^2-2akx+ka^2+b. Si agafo, com a exemple, la paràbola y=2x^2-8x+10 (la que hi ha d'exemple al lloc d'on he robat la imatge i tot això... ja no ve d'aquí), es pot posar com y = 2(x-2)^2+2. Si la paràbola en qüestió no talla l'eix de les x, k i b tenen el mateix signe. El vèrtex de la paràbola es troba a x=a.

La paràbola simètrica a la que tinc respecte del vèrtex és y=-k(x-a)^2+b. Aquesta tallarà l'eix de les x en dos punts, que són x=a+sqrt(b/k) i x=a-sqrt(b/k).

Els punts de la circumferència centrada al punt (a,0) i de radi sqrt(b/k) que passen per la recta x=a són (a, sqrt(b/k)) i (a, -sqrt(b/k)).

Quines són les arrels de la paràbola inicial? No cal descomposar i aplicar la fórmula, simplement:

k(x-a)^2+b=0

k(x-a)^2=-b

(x-a)^2=-b/k

Com que b i k tenen el mateix signe, la part de la dreta de la igualtat és negativa, així que fent l'arrel, sortiran complexes:

x-a= +-sqrt(b/k)i

I, per tant, les solucions són x = a +- sqrt(b/k)i, que són exactament les que s'han representat en el pla complex mitjançant la paràbola simètrica i la circumferència.

Problema d'escacs - 8 agost

Juguen blanques i guanyen:

Problema d'escacs - 7 agost

Juguen blanques i guanyen:

Problema d'escacs - 6 agost

Negres juguen i guanyen:

(la posició està posada des del punt de vista de les blanques: les blanques van cap amunt i les negres, cap avall)

Problema d'escacs - 5 agost

Blanques juguen i guanyen:

Problema d'escacs - 4 agost

Blanques juguen i guanyen:

Problema d'escacs - 3 agost

Negres juguen i guanyen:

(continua essent facilet...)

Persèides

Com cada any, a mitjans d'agost, el cel ens regala la pluja d'estrelles de les Persèides.

Aquest any, la màxima freqüència de meteors es produirà el 12 d'agost a mitja tarda, però com que serà clar no es veuran. Així doncs, el millor dia per veure'n serà la nit del 12 al 13 d'agost. De totes formes, com que la pluja es veu uns dies abans i uns dies després, doncs qualsevol dia proper al 12 és bo per veure-la (és clar que amb menys freqüència de meteors que el dia 12).

La pluja de les Persèides es diu precisament així perquè els meteors semblen provenir de la constel.lació de Perseus, a prop de Cassiopea. Aquesta constel.lació es troba cap al nord/nord-est. Al principi de la nit està més baixa, i a mida que va avançant la nit va pujant la seva alçada respecte a l'horitzó.

Els meteors de les Persèides procedeixen del cometa Swift-Tuttle, que té una òrbita que passa per on passa l'òrbita de la Terra cap a l'11 o 12 d'agost. Com tots els cometes, quan s'acosta al Sol, es va desintegrant i deixant restes. Les Persèides no són res més que aquests trossos de cometa, que són atrets per la gravetat de la Terra i al caure, es tornen incandescents amb pel fregament amb l'atmòsfera.

Problema d'escacs - 2 agost

Juguen blanques i guanyen:

Problema d'escacs - 1 agost

Per cel.lebrar que aquest mes molta gent està de vacances, posaré cada dia un problema d'escacs (facilet). Com sempre, els comentaris estan oberts per si algú vol posar la solució a qualsevol dels problemes.

En el problema d'avui, juguen blanques i guanyen: