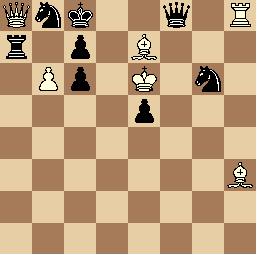
Començo mirant el següent final de peons:

En aquest cas juguen blanques. Les blanques tenen un peó a sisena, mentre que el de les negres està a segona. En principi, això seria bo pel blanc, però si ens mirem una mica millor la posició, veiem que el peó de b6 es perd irremediablement. Si el blanc intenta anar a defensar-lo, 1. Rf4 Rd3 2. Re5 Rc4 3. Rd6 Rb5 4. Rc7, el negre el guanya simplement jugant Ra6.
Així doncs, amb el peó de b6 perdut, el blanc intentarà fer taules. Però, com s'aconsegueixen les taules? Doncs la forma de fer-ho és col.locant-se a b4 just quan el rei negre acabi de menjar el peó de b6. Per tant, l'objectiu del blanc és poder arribar a b4. I quina és la forma més ràpida d'arribar-hi? Doncs, encara que sembli mentida, la forma més ràpida d'arribar-hi és mitjançant les diagonals g3-e1 i e1-b4.
Ja hem vist que amb Rf4 no s'aconseguia arribar a b4 a temps. I què passaria si el blanc jugués 1. Rf3, que en principi està més a prop de b4 que f2? Si el blanc jugués 1. Rf3, el negre podria jugar 1. ... Rd3! tapant el pas del blanc cap a b4.
Així que la única solució és 1. Rf2! Rd3 2. Re1 Rc4 3. Rd2 Rb5 4. Rc3 Rxb6 i arribem a temps a jugar 5. Rb4 taules. Si el negre ens hagués volgut tapar la diagonal jugant 1. ... Rd2, simplement juguem 2. Rf1. A 2. ... Rd3 o Rc3 es contesta 3. Re1, com abans, arribant a temps a b4. A 2. ... Rd1 es contesta 3. Rf2 i també s'arriba a temps a b4.
El següent final és semblant al que acabo d'explicar:

El peó negre d'h7 està perdut. Així doncs, les negres no poden aspirar a res més que a fer taules. Per fer taules, han d'aconseguir portar el seu rei a f7 just en el moment en què les blanques mengin el peó d'a7. Per fer-ho, altra vegada s'ha d'utilitzar una diagonal, en aquest cas la diagonal a2-g8.
Si el negre jugués 1. ... Rc1, perderia i no podria arribar a f7 a temps: 2. Rc3! Rb1 3. Rd4 Rc2 4. Re5 Rd3 5. Rf6 Re4 6. Rg7 Rf5 7. Rxh7 Rf6 8. Rg8.
Però el negre pot aconseguir les taules mitjançant 1. ... Ra1! 2. Rc3 Ra1 3. Rd4 Rb3 4. Re5 Rc4 5. Rf6 Rd5 6. Rg7 Re6 7. Rxh7 i arriba just a temps per jugar 7. ... Rf7 i taules.
Sí, ja ho sé, són finals senzills que la majoria ja hem vist alguna vegada o alguna altra. Però sovint les coses s'obliden, o en una partida real no tenim a ningú al cantó que ens digui: "Mira, aquesta és una posició de problema". Així que com més vegades els veiem, més possibilitats tenim de recordar-nos-en.
Després d'aquests dos finals de peons que eren taules, en veurem dos més amb peons de torre que es guanyen per part de les blanques i un altre que el deixaré com a problema. El primer dels que guanyen les blanques és el següent:

Aquest final s'assembla a l'anterior. El peó d'h7 està perdut. Si les negres aconsegueixen arribar a f7 en el moment en què les blanques es mengin el peó d'h7, seran taules. Les blanques han de lluitar per poder-se menjar el peó, impedint a la vegada que el negre arribi a f7 a temps.
Com abans, el negre intenta agafar la diagonal a2-g8, que li donaria les taules. El blanc li ho impedeix: 1. Rd6 Rf3 2. Re5! única per impedir al negre arribar a temps a la diagonal. Si 2. Re6 Re4 3. Rf6 Rd5 i arriba a la diagonal. 2. ... Re3 3. Rf6 Re4 4. Rg7 Rf5 5. Rxh7 Rf6 6. Rg8 i les blanques guanyen.
Ja per últim, en el següent final, també guanyen les blanques:

Si les blanques intenten 1. h4, no arriben a temps, perquè el negre aconsegueix arribar a temps a la casella f7. Per exemple 1. ... Rd3 2. h5 Re4 3. h6 Rd5 i aconsegueix arribar a la diagonal. Tampoc serveix 3. Rg7 Rf5 4. Rxh7 Rf6 i taules.
Tampoc els serveix a les blanques anar a menjar el peó mitjançant la maniobra Rg5-h6. Per exemple, 1. Rg5 Rd3 2. Rh6 Re4 3. Rxh7 Rf5 i taules.
La solució és jugar 1. Rg7!, que malgrat sembla que perdi temps, ja que el negre pot jugar 1. ... h5, el blanc aconsegueix arribar a temps a g7. 2. Rg6 h4 (si 2. ... Rd3 3. Rxh5 Re4 4. Rg6 i el blanc corona). 3. Rg5 h3 (si 3. ... Rd3 4. Rxh4 Re4 5. Rg5 guanyant) 4. Rg4 Rd3 5. Rxh3 Re4 6. Rg4 i el blanc corona.
Ja per acabar, un problema que no té massa a veure amb els anteriors, excepte que és un final de peons.
A la següent posició, juguen blanques i guanyen:

Sí, realment sembla que les blanques estan molt millor, però no s'han de desestimar les possibilitats defensives derivades de la jugada 1. ... h5.
El deixo com a problema, per si algú se'l vol pensar. No és excessivament difícil, però s'ha d'anar una mica amb compte.