Anàlisis Matgala - James Stack

Ja fa un temps li vaig prometre a en James que analitzaria aquesta partida, que vam jugar a gameknot. I he pensat que seria una bona idea de posar-la aquí, per si algú més té alguna altra cosa a dir. És clar que com que en James només parla anglès i rus (i jo, de rus, res de res), doncs hauré d'escriure els comentaris en anglès (i demano perdó per anticipat per les faltes).

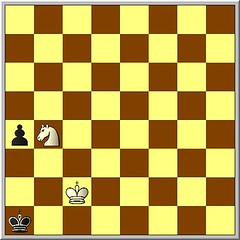
I will insert in the game my comments (in red) and James' comments (in green).

1. e4 e6 2. d3 c5 3. Nf3 g6 4. g3 Bg7 5. Bg2 Nc6
6. O-O d6 7. c3 Nge7 8. Nbd2 O-O 9. Re1 b5 10. Nf1 a5
11. Bg5 b4 12. Qc2 Bd7 13. Rad1 h6

After 13..h6 I was already a little worse. (13..Qb6 would have led to a more interesting game I think.)And after 14. Bf4 e5 15. Be3 I was felt I was definitely losing. It was so bad I felt it necessary to sacrifice a pawn and hope for complications.

14. Bf4 e5 15. Be3 Kh7
16. d4 f5

I think that here black doesn't need to sacrifice a pawn. After 16. ... cxd4 17. cxd4 Rc8, there is no problem for black.

17. dxc5 fxe4 18. Qxe4 d5

I felt you had 2 good chances to win. Once in the middlegame and once in the endgame. I thought In the middlegame after 18..d5 you should play 19. Qh4 where if I try 19..Rf5 20. g4 is excellent for white.

19. Qc2 bxc3 20. bxc3 Bg4

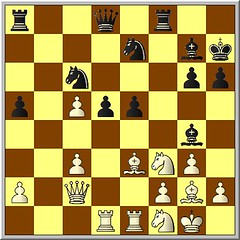
Here I have to considere 21. c4. After 21. ... Bxf3 22. Bxf3 Rxf3 23. cxd5, the passed pawns are a good compensation for the piece, but I don't know if they are enough. I loose a piece or a quality anyway, so this option seems better than the one I played.

21. Nf1d2 e4 22. Nd4 Bxd1 23. Rxd1 Qd7 24. Nxc6 Nxc6


I think that here the better move for white was 25. Nxe4. Now it is very clear for me. I don't know what I didn't played it in the game. After it, 25. ... Qf5 is not valid for Rxd5.

25. Qc1 Qg4
26. Nf1 Rae8 27. Rxd5 Ne5 28. Bd4 Nf3+

It was interesting to play 28. ... Qf5

29. Bxf3 exf3 30. Ne3 Rxe3
31. Bxe3 Bxc3

Here I can play 32. c6 and I think that after 33. Rc5, I have more chances to win than with the move I did in the game.

32. Qd1 Rf7 33. c6 Qh3 34. Qf1 Qe6 35. Rc5 Be5
36. Qc4 Qxc4 37. Rxc4 Bc7

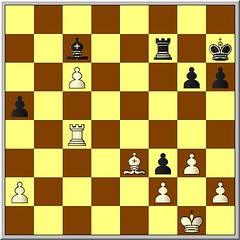
Then in the ending after we exchanged queens I thought you could have obtained a winning advantage with 38. Bf4 BxB 39. pxB Rc7 40. h4 where your plan should be to walk your king over to the kingside take the pawn on f3 and continue to walk closer to my other kingside pawns. I can't move my rook until my king gets close to my rook

For instance, the following variation may be reasonable.
[ 38.Bf4 Bxf4 39.gxf4 Rc7 40.h4 Kg7 41.Kh2 Kf7 42.Kg3 Ke7 43.Kxf3 Kd6 44.Ke4 Re7+ 45.Kd4 Rc7 46.a4 Rxc6 47.Rxc6+ Kxc6 48.Ke5 Kc5 49.Kf6 Kb4 50.Kxg6 Kxa4 51.f5 Kb3 52.f6 a4 53.f7 a3 54.f8Q a2]

I agree with you. Looking at this position now, it seems difficult that white loose the advantadge.

38. Rd4 g5 39. Kf1 Kg6 40. Ke1 Rf6
41. Rc4 Kf5 42. h3 Ke6 43. Kd2 Kd5 44. Rc5+ Kd6 45. Rc2 Kd5
46. Kd3 Rxc6 47. Rxc6 Kxc6 48. Ke4 Kb5

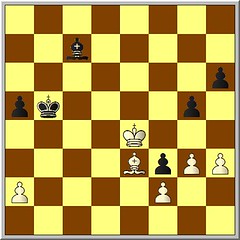
I think that here I lost the last chance to win the game. I did a bad calculation and I thought I couldn't take the f3 pawn. But it was enough to win.

49. Bc1 Bxg3 Good! It was a surprise for me.50. Kxf3 Bd6
51. Kg4 Kc4 52. h4 gxh4 53. Bxh6 Kb4 54. f4 Ka3 55. f5 Kxa2
56. Kxh4 1/2-1/2

Maslesha - V. Raicevic, Sarajevo 1978

L'altre dia, mirant-me unes línies de la francesa, vaig anar a parar a aquesta partida. Sembla que les blanques ho tenen tot de cara per fer el sacrifici Ah7, però les negres aconsegueixen sortir-se'n.

La partida va començar de la següent forma, fins a arribar a la posició del diagrama:

1. e4 e6 2. d4 d5 3. Cc3 Cf6 4. Ag5 Ae7 5. e5 Cfd7 6. Axe7
Dxe7 7. Dd2 O-O 8. f4 c5 9. dxc5 Cc6 10. Cf3 Dxc5 11. O-O-O Tb8 12. Ad3 b5

A la posició del diagrama sembla que la jugada 13. Axh7+ s'escapa de les mans. Tot i que en aquesta partida no va ser fructífer.

13. Axh7+ Rxh7 14. Cg5+ Rg8! Única jugada possible en aquest cas. A partir d'aquí, el blanc segueix amb el seu atac: 15. Dd3 Te8! Jugada única. 15. ... Td8 no serveix per 15. Dh7+ Rf8 16. Dh5 g6 17. Cdxe5 Rb1! i el negre recupera la peça entregada, quedant amb superioritat. 16. Dh7 Rf8

Observem que ara Dh5 no val per Cd8.

En aquest cas, sembla que la jugada més correcta seria 17. Dh8+, seguit de Re7 17. Dh4, conservant atac per la peça entregada, i amb molt bones possibilitats. Però el blanc va subestimar les possibilitats del negre i va jugar 17. The1, deixant que les negres consolidessin la seva posició i acabessin guanyant amb la peça de més que tenien. La partida va continuar: 17. ... Cd4 18. Dh5 Re7! 19. Dxf7+ Rd8 20. Txd4 Dxd4 21. Cxe6+ Txe6 22. Dxe6 Dxf4+ 23. Rb1 Tb6 24. Dxd5 Ab7 25. Dd3 Dc4 26. Df5 De6 27. Dg5+ De7 28. Dd2 a6 29. Cd5 Axd5 30. Dxd5 Rc7 31. Da8 Cc5 32. Dd5 Te6 33. a3 Cd7 34. Da8 Rb6 35. g3 Txe5 36. Txe5 Dxe5 37. Dd8+ Dc7 38. De7 Ce5 39. Dg5 Cc4 40. Dg6+ Ra7 41. Dd3 De5 42. Dd7 Rb6 43. Dd8+ Rc6 44. Da8+ Rd7 45. Db7+ Re8 46. Dc6+ Rf7 47. Dd7+ Rf6 48. Dc6+ Rg5 49. c3 De2 50. Dd5+ Rh6 0-1

El problema de la setmana - 9 dames

La majoria de la gent ja coneix el problema de les vuit dames: consisteix a posar 8 dames en un tauler d'escacs, de forma que cap d'elles amenaci a cap de les altres dames.

El problema d'aquesta setmana és una variació del problema de les 8 dames (i una mica més difícil, per cert). Es tracta de col.locar 9 dames en un tauler d'escacs (8x8, per si de cas...) de forma que cap dama amenaci a cap altra dama. I, com que només hi ha 8 files i 8 columnes, es permet posar "peons" que facin de barrera entre dues dames.

Es tracta de posar les 9 dames, utilitzant el mínim nombre de peons "barrera".

Aquesta setmana donaré 3 punts (en cas de que algú doni amb la solució):

- Posar les 9 dames, utilitzant 3 peons. Aquesta és bastant fàcil, usant com a base la solució de 8 dames, i afegir una dama flanquejada per 3 peons en una punta (estic donant moltes pistes).

- Posar les 9 dames, utilitzant 2 peons.

- Posar les 9 dames, utilitzant 1 peó.

Aquesta setmana (crec) el problema és complicat (bé, amb 3 peons no ho és tant).


Setmana anterior

Setmana següent

Cavall contra peó

Aquest problema m'ha agradat pel fet de que el blanc, només tenint un cavall, aconsegueix guanyar la partida. No és difícil. A la següent posició, juguen blanques i guanyen.

La solució com a comentari en uns minutets.

La llei de Benford

Imagina que tens poca feina. Molt poca feina. I que un diumenge qualsevol llegeixes un diari d'una punta a l'altra i vas anotant en un paper tots els números que surten (el resultat dels partits, les hores de la cartellera de cine, la gent que va anar a no sé on, ... tots els números). Un cop tens tots els números ben anotats, els separes en 9 columnes: una amb els números que comencen en 1, una altra amb els que comencen en 2, i així fins a una columna pels números que comencen per 9.

Creus que totes les columnes tindran el mateix número de números? Alguna columna serà més nombrosa que les demés?

Un cop has fet això, agafes un atles i busques la llargada de tots els rius que trobis. Quina columna és més nombrosa? Són totes iguals? I si ho fas amb l'alçada de muntanyes? O amb la població dels pobles de Catalunya? O amb qualsevol altra cosa que se't pugui ocórrer?

En principi, el sentit comú ens diria que totes les columnes tindrien aproximadament un 11.11% dels números. Però segons la llei de Benford això no és així. Els números que comencen amb 1 són aproximadament un 30%, els que comencen amb 2 són aproximadament un 17%, els que comencen amb 4, un 12%. El percentatge es va reduint mentre augmenta la xifra per la que comença el número, fins a arribar al 9, que té menys d'un 5% dels números.

A l'enllaç que he posat abans hi ha una demostració del fenomen, utilitzant models estadístics. Si més no, és curiós.

La Voyager 1 arriba als límits del Sistema Solar

La Voyager 1 va ser llançada a l'estiu de l'any 1977 (alguns encara no havíem nascut...) per estudiar Júpiter i Saturn i els seus satèl.lits. En principi, tenien una vida esperada d'uns 5 anys. Però la missió anava essent un èxit, i tant la Voyager 1 com la 2 van seguir allunyant-se de la Terra, estudiant Urà i Neptú.

Després de deixar Neptú, es va decidir enviar els Voyagers encara més lluny, fins als límits del Sistema Solar.

Ara, gairebé 28 anys després del seu llançament, la Voyager 1 ha arribat als límits del Sistema Solar. Tal com es veu al gràfic, ha arribat o està a prop del "termination shock". Aquesta és una zona en la que el vent solar es torna bastant més lent.

Degut a diferents fenomens físics que s'han observat al voltant de la Voyager 1, els científics han deduit que havia arribat a aquesta zona.

Més informació aquí.

El problema de la setmana - Mat en mitja jugada

Després d'un problema de la setmana una mica complicat, aquesta setmana el problema és bastant fàcil (o això crec), almenys per la gent que sap jugar a escacs.

El problema està tret del llibre "El tablero mágico", de Carlo Frabetti, que és un llibre on hi ha jocs d'ingeni basats en el tauler i les peces dels escacs.

En el tauler següent, les blanques juguen i donen mat en mitja jugada.

Suposo que hi haurà resposta. Si no n'hi ha, donaré la solució dissabte 28 o diumenge 29.

Setmana anterior

Setmana següent

Internet puzzle solvers test (IPST)

Demà comença la segona ronda de l'IPST. És una iniciativa interessant, és clar que s'ha de tenir temps per pensar-se els problemes.

Els problemes es penjaran a la pàgina de Diogen i es poden resoldre durant una setmana.

Els problemes no són fàcils, són d'aquells en els que t'hi has de passar una estona (si fossin fàcils, quina gràcia tindria?) I, és clar, una setmana és poquet temps per resoldre'ls tot (sinó, on seria la gràcia?) A la ronda anterior hi havia 12 problemes, que significa que s'han de resoldre gairebé dos problemes al dia (realment, s'ha de tenir molt de temps, o ser molt bo resolent problemes). Tot i així, encoratjo a tothom a participar-hi (cosa que jo no faré) o, com a mínim a d'aquí un temps (o mentre es fa el test) intentar resoldre'n algun (cosa que sí faré).

Sort a qui hi participi!

Més jocs educatius

Fa uns quants dies vaig parlar-vos de Cyberchase. Avui li toca el torn a KidsPsych. Són jocs per nens petits, amb alguna explicació del que es fa pels pares.

Els jocs estan dividits en dos menús, un menú amb jocs més senzills (del tipus de reconèixer formes i colors) per nens d'1 a 5 anys.

Els altres jocs són per nens de 6 a 9 anys. Entre ells, hi ha el joc de passar una gallina, una guineu i una bossa de gra d'una banda a l'altra de riu sense que ningú es mengi a ningú. També hi ha un joc amb cares que m'ha fet riure molt.

El problema de la setmana. 15/05/05-22/05/05

Aquesta setmana el problema me l'ha proposat l'Omalaled. Es tracta d'aconseguir el número 21 utilitzant els números 1, 5, 6 i 7. Aquests números s'han d'utilitzar un cop cada un (i només un cop) i només es poden utilitzar les operacions bàsiques (suma, resta, multiplicació i divisió).

Val a dir que el problema no és tan senzill com sembla (o potser sí?) Així que donaré una pista. Tot i que les meves pistes a vegades serveixen més per embolicar la troca que per res més. De totes formes, aquí va: l'operació en la que es basa la solució va ser una de les primeres que se'm va acudir. Però la vaig desestimar de seguida, perquè hi havia un número que feia servir dos cops i un altre que no feia servir. La solució era tan fàcil com arreglar aquella idea que vaig tenir. No sé si embolica més o no. Quan algú dongui la solució, si no ho explica, ja ho explicaré jo. Si ningú dóna la solució, diumenge 22 ja la donaré jo.


Setmana anterior

Setmana següent

El problema de la setmana - 8/05/05 - 15/05/05

Després d'uns mesos sense problema de la setmana, avui torna. Un problema senzillet, a veure què tal.

Es tracta de moure la posició de NOMÉS UN DÍGIT de la següent expressió matemàtica, de forma que es compleixi la igualtat:

101 - 102 = 1

Si no hi ha solució, diumenge que ve la posaré com a comentari.

He afegit una classificació al link del problema de la setmana, per si a algú li agrada estar a dalt de tot de la llista, que s'espavili a contestar. També he afegit un link als problemes de la setmana més comentats.

Setmana anterior

Setmana següent

3816547290

Avui he descobert un blog molt interessant, el blog d'en Markelo. Un dels temes que més m'han agradat ha sigut el de números extraordinaris. Segur que hi torno. M'han agradat especialment les explicacions sobre els números 153 i 6174. Segur que hi torno. I segur que em poso a mirar les raons per les que aquests números són extraordinaris. Però avui, per començar, parlaré d'un altre número (també tret d'aquesta pàgina), el 3816547290.

Què té d'especial aquest nombre? Molt fàcil:

- És un número pandigital (la parauleta vol dir que conté tots els dígits).
- 3 és divisible per 1.
- 38 és divisible per 2.
- 381 és divisible per 3.
- 3816 és divisible per 4.
- 38165 és divisible per 5.
- 381654 és divisible per 6.
- 3816547 és divisible per 7.
- 38165472 és divisible per 8.
- 381654729 és divisible per 9.
- 3816547290 és divisible per 10.
- És l'únic número que compleix aquestes condicions.

Que les compeleix està clar. Anem a veure que realment és l'únic:

- Com que el nombre complet ha de ser divisible per 10, l'últim dígit del número ha de ser un 0: el número serà *********0.

- Com que el número format per les dues primeres xifres ha de ser divisible per 2, el segon dígit ha de ser parell. Com que el número format per les 4 primeres xifres ha de ser divisible per 4, el quart dígit ha de ser parell. De la mateixa forma, el 6è i 8è dígits han de ser parells. L'últim dígit és un 0. Per tant, només queden 4 dígits parells. Així doncs, a les posicions parells hi haurà números parells (p) i a les senars, números senars (s): el número serà spspspsps0.

- Com que el número format amb les 5 primeres xifres ha de ser divisible per 5, la cinquena xifra ha de ser un 5 (el 0 ja està posat, i sabem que ha de ser senar): El número ha de ser spsp5psps0.

- La primera xifra sempre serà divisible per 1, sigui quina sigui. Per tant, no ens preocupem més d'aquesta condició.

- El nombre format per les 9 primeres xifres serà divisible per 9, ja que 1+2+3+4+5+6+7+8+9 = 45 = 9*5. Per tant, tampoc ens preocupem per aquesta condició.

- Les 3 primeres xifres han de sumar un múltiple de 3.
Les 6 primeres xifres han de sumar un múltiple de 3. Això vol dir que les xifres que estan en les posicions 4, 5 i 6 han de sumar un múltiple de 3.
Les 9 primeres xifres sumen un múltiple de 3. Per tant, les xifres en les posicions 7, 8 i 9 també han de sumar un múltiple de 3.

- Donat que a la posició 5 hi ha d'haver un 5 i que a les posicions 4 i 6 hi ha d'haver números parells, i les 3 han de sumar un múltiple de 3, tenim les següents possibilitats:
- 258
- 456
- 654
- 852

- De la mateixa forma, les 3 primeres i les 3 últimes xifres han de ser un d'aquests números:
(la primera xifra ha de ser senar, la segona xifra ha de ser parell, i la tercera, senar; les 3 xifres han de sumar un múltiple de 3; no hi poden haver xifres repetides; no hi pot haver ni 0 ni 5).
- 123
- 129
- 147
- 183
- 189
- 321
- 327
- 369
- 381
- 387
- 723
- 729
- 741
- 783
- 789
- 921
- 927
- 963
- 981
- 987

- I ara s'han de combinar aquests números. S'han d'escollir dos blocs d'aquests últims pel primer i el tercer i un bloc dels anteriors pel segon. No hi ha d'haver cap número repetit i s'han de complir les condicions que encara falten per complir-se:
- Les 4 primeres xifres han de ser un múltiple de 4 (cond1).
- Les 8 primeres xifres han de ser un múltiple de 8 (cond2).
- Les 7 primeres xifres han de ser un múltiple de 7 (cond3).

- Segon bloc: 258. Els altres dos blocs només poden ser: 147, 369, 741 i 963.
Possibilitats:
- 147 258 369: No es compleix la cond2.
- 147 258 963: No es compleix la cond3.
- 369 258 147: No es compleix la cond2.
- 369 258 741: No es compleix la cond2.
- 741 258 369: No es compleix la cond2.
- 741 258 963: No es compleix la cond3.
- 963 258 147: No es compleix la cond2.
- 963 258 741: No es compleix la cond2.

- Segon bloc: 852. Els altres blocs només poden ser 147, 369, 741 i 963. Amb cap d'aquests blocs com a primer bloc es compleix la cond1, ja que ni 78, ni 98, ni 18, ni 38 són divisibles per 4. Així que aquest bloc també el podem el.liminar.

- Segon bloc: 456. Els altres blocs poden ser: 123, 129, 183, 189, 321, 327, 381, 387, 723, 729, 783, 789, 921, 927, 981, 987.
Perquè les 4 primeres xifres siguin múltiples de 4, el primer bloc ha d'acabar en un nombre parell. I això és impossible. Així que ja hem descartat aquest bloc.

- El número serà de la forma: sps654sps0. Amb això, queda garantida la cond1.

- Perquè es compleixi la cond2, el tercer bloc només pot ser: 321, 327, 723, 729. Així doncs, les possibilitats (a les que només cal comprovar que el número format amb les 7 primeres xifres sigui múltiple de 7) són:
- 789 654 321
- 987 654 321
- 189 654 327
- 981 654 327
- 189 654 723
- 981 654 723
- 183 654 729
- 381 654 729

D'aquests, només l'últim compleix la condició.

Per tant, l'únic número que compleix TOTES les condicions és el 3816547290. Al final, la demostració que era únic m'ha sortit massa llarga. Si algú té alguna idea per una demostració més curta, serà benvinguda.

Road sign math

Road sign math és un joc que serveix per fer els viatges més amens. És una iniciativa que pretén entretenir alhora que educar. Es tracta simplement de fixar-se en els cartells que es troben a les carreteres i intentar trobar relacions entre els números que indiquen les distàncies a les ciutats i/o els números de carretera.

Les curiositats que es puguin trobar es poden enviar a la seva pàgina web (en anglès):

Com a exemple, algunes de les imatges que s'han enviat:

A la següent imatge, es pot observar que multiplicant els dos primers nombres surt el segon:

Fins i tot alguna d'una mica més complicada: 315/45 + 14 = 21:

També hi ha la possibilitat d'enviar coses més complicades, com el factorial que apareix al següent cartell:

O algun tipus de sèrie, com la de Fibonacci

o els quadrats:

No hi ha límit a l'imaginació. Només es tracta d'observar, calcular i trobar relacions entre els nombres.

Arimaa (2)

Ja fa uns quants dies que vaig parlar d'arimaa. Ho havia deixat una mica abandonat, però ara hi torno, amb unes quantes regles del joc i amb com s'anoten les jugades.

Notació de jugades:

Les peces s'escriuen mitjançant lletres majúscules i minúscules. Les lletres majúscules corresponen a les peces daurades i les minúscules a les platejades.

Cada peça diferent està notada per la seva inicial. Tal com vaig fer amb els escacs gòtics, i ja que no he trobat cap pàgina web que parli de l'arimaa en català, doncs jo m'invento les inicials: Elefant (E), caMell (M), Cavall (C), Gos (G), GaT (T) i coNill (N) (coi, és que la majoria de noms havien de començar amb c o g?)

Les files i columnes es numeren com en els escacs. Les peces daurades surten de les files 1 i 2 i les peces platejades surten de les files 7 i 8.

Cada torn de jugada es posa en una línia. Al començar la línia s'hi ha de posar el número de jugada i el color, i llavors les jugades que es fan. Per escriure un moviment només cal escriure la inicial de la peça, seguida de la casella a on està col.locada, i per últim s'hi posa la direcció cap on va (Nord, Sud, Est o Oest).

Per indicar una captura, es fa com en els escacs, amb el símbol x.

No he trobat enlloc que s'hagi d'indicar com es col.loquen les peces en iniciar la partida. Trobo que estaria bé saber-ho. Tot i que potser s'ha de posar i jo no ho he vist...

Algunes regles de l'arimaa:

- Quan tots dos jugadors perden tots els seus conills, la partida és declarada taules (lògic, d'altra banda).

- En cap moment es poden acordar taules. O guanya un, o guanya l'altre, o es queden sense conills.

- Si un jugador es queda en situació d'ofegat (no pot moure cap de les seves peces) aleshores el jugador perd la partida.

- Si un jugador repeteix 3 vegades la mateixa posició al finalitzar una jugada, aleshores el jugador que ha repetit la posició per tercera vegada perd la partida.

- Un jugador pot moure un conill contrari fins a la seva primera fila (vuitena del rival) sense perdre la partida, sempre i quan, quan acabi el seu torn, el conill ja no estigui a la vuitena fila.

Com a conclusió a aquestes regles, doncs sembla que es vol evitar bastant les taules: dues situacions que són taules en els escacs aquí no ho són. I no es poden acordar. La única forma de fer taules és que ambdós jugadors perdin tots els seus conills, cosa que no sembla massa fàcil.